Question

【题目】如图，一次函数y=kx+b（k≠0）与反比例函数y= （m≠0）的图象有公共点A（1，2），D（﹣2，﹣1）．直线l⊥x轴，与x轴交于点N（3，0），与一次函数和反比例函数的图象分别交于点B，C．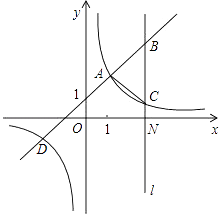
（1）求一次函数与反比例函数的解析式；
（2）求△ABC的面积；
（3）根据图象回答，在什么范围时，一次函数的值大于反比例函数的值．

Answer 1

【答案】
（1）解：把（1，2）代入y= 得m=2，

则反比例函数的解析式是y= ；

根据题意得 ，

解得 ，

则一次函数的解析式是y=x+1

（2）解：在y= 中，令x=3得y= ，则C的坐标是（3， ），

在y=x+1中令x=3，则y=4，B的坐标是（3，4）．

则BC=4﹣ = ．

则S△ABC= × ×（3﹣1）=

（3）解：一次函数的值大于反比例函数时x的范围是：﹣2＜x＜0或x＞1
【解析】（1）利用待定系数法即可求得函数的解析式；（2）首先求得B和C的坐标，则BC的长即可求得，然后利用三角形的面积公式求解；（3）求一次函数的值大于反比例函数时x的范围就是求一次函数的图象在反比例函数的图象的上边部分对应的自变量x的范围．