ЬтФПФкШн
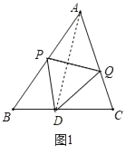
ЁОЬтФПЁПШчЭМЕФЁїABCжаЃЌABЃОACЃОBCЃЌЧвDЮЊBCЩЯвЛЕуЁЃЯжДђЫудкABЩЯеввЛЕуPЃЌдкACЩЯеввЛЕуQЃЌЪЙЕУЁїAPQгывдPЁЂDЁЂQЮЊЖЅЕуЕФШ§НЧаЮШЋЕШЃЌвдЯТЪЧМзЁЂввСНШЫЕФзїЗЈЃК
МзЃКСЌНгADЃЌзїADЕФжаДЙЯпЗжБ№НЛABЁЂACгкPЕуЁЂQЕуЃЌдђPЁЂQСНЕуМДЮЊЫљЧѓЃЛ
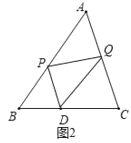
ввЃКЙ§DзїгыACЦНааЕФжБЯпНЛABгкPЕуЃЌЙ§DзїгыABЦНааЕФжБЯпНЛACгкQЕуЃЌдђPЁЂQСНЕуМДЮЊЫљЧѓЃЛ
ЖдгкМзЁЂввСНШЫЕФзїЗЈЃЌЯТСаХаЖЯКЮепе§ШЗЃЈЁЁЁЁЃЉ?

A.СНШЫНде§ШЗB.СНШЫНдДэЮѓC.Мзе§ШЗЃЌввДэЮѓD.МзДэЮѓЃЌвве§ШЗ
ЁОД№АИЁПA
ЁОНтЮіЁП
ШчЭМ1ЃЌИљОнЯпЖЮДЙжБЦНЗжЯпЕФаджЪЕУЕНPA=PDЃЌQA=QDЃЌдђИљОнЁАSSSЁБПЩХаЖЯЁїAPQЁеЁїDPQЃЌдђПЩЖдМзНјааХаЖЯЃЛШчЭМ2ЃЌИљОнЦНааЫФБпаЮЕФХаЖЈЗНЗЈЯШжЄУїЫФБпаЮAPDQЮЊЦНааЫФБпаЮЃЌдђИљОнЦНааЫФБпаЮЕФаджЪЕУЕНPA=DQЃЌPD=AQЃЌдђИљОнЁАSSSЁБПЩХаЖЯЁїAPQЁеЁїDQPЃЌдђПЩЖдввНјааХаЖЯЃЎ
ШчЭМ1ЃЌЁпPQДЙжБЦНЗжADЃЌ
ЁрPA=PD,QA=QD,
ЖјPQ=PQЃЌ
ЁрЁїAPQЁеЁїDPQ(SSS)ЃЌЫљвдМзе§ШЗЃЛ
ШчЭМ2,ЁпPDЁЮAQ,DQЁЮAPЃЌ
ЁрЫФБпаЮAPDQЮЊЦНааЫФБпаЮЃЌ
ЁрPA=DQЃЌPD=AQЃЌ
ЖјPQ=QPЃЌ
ЁрЁїAPQЁеЁїDQP(SSS)ЃЌЫљвдвве§ШЗЁЃ
ЙЪбЁЃКA.