题目内容
【题目】已知,如图,点A、D、B、E在同一直线上,AC=EF,AD=BE,∠A=∠E,
(1)求证:△ABC≌△EDF;
(2)当∠CHD=120°,猜想△HDB的形状,并说明理由.

【答案】(1)见解析;(2)△HDB为等边三角形;理由见解析;
【解析】
(1)根据SAS即可证明:△ABC≌△EDF;
(2)由(1)可知∠HDB=∠HBD,再利用三角形的外角关系即可得三角形HDB为等边三角形.
(1)证明:
∵AD=BE,
∴AD+DB=BE+DB,
∴AB=ED,
在△ABC和△EDF中,
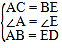 ,
,
∴△ABC≌△EDF(SAS);
(2) △HDB为等边三角形,理由如下:
∵△ABC≌△EDF,
∴∠HDB=∠HBD,
∵∠CHD=∠HDB+∠HBD=120°,
∴∠HDB=∠HBD=60°,
∠DHB=60°.
∴△HDB为等边三角形.

练习册系列答案
相关题目