题目内容
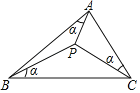
【题目】如图,若△ABC内一点P,满足∠PAB=∠PBC=∠PCA=α,则称点P为△ABC的布洛卡点.通过研究一些特殊三角形中的布洛卡点,得到如下两个结论:
①若∠BAC=90°,则必有∠APC=90°;②若AB=AC,则必有∠APB=∠BPC.
对于这两个结论,下列说法正确的是( )
A.①对,②错B.①错,②对C.①,②均错D.①,②均对
【答案】D
【解析】
由直角三角形的性质可判断①,通过证明△ABP∽△BCP,可判断②.
解:若∠BAC=90°,
∴∠BAP+∠PAC=90°,且∠PAB=∠PBC=∠PCA=α,
∴∠PAC+∠ACP=90°,
∴∠APC=90°,故①对,
若AB=AC,
∴∠ABC=∠ACB,且∠PAB=∠PBC=∠PCA=α,
∴∠ABP=∠BCP,且∠BAP=∠PBC,
∴△ABP∽△BCP,
∴∠APB=∠BPC,故②对,
故选:D.

练习册系列答案
相关题目