题目内容
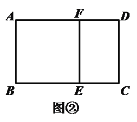
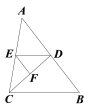
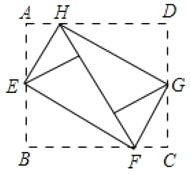
【题目】如图，将矩形ABCD的四个角向内翻折后，恰好拼成一个无缝隙无重合的四边形EFGH，EH=12cm，EF=l6cm则边AD的长是（ ）
A.12cmB.16cmC.20cmD.24cm
【答案】C
【解析】
根据图示，△HEF为直角三角形，EH=12cm，EF=16cm，则勾股定理可得HF=20cm，再由图形变化可知AD=AH+HD=HF=20cm．
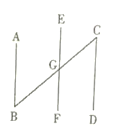
如图所示，由折叠过程可知：∠AEH=∠HEM，∠MEF=∠BEF，
∵∠AEH+∠AHE=90°，∠HEM+∠MEF=90°，
∴∠MEF=∠BEF=∠AHE，同理可得∠EHM=∠DGH=∠GFN，
∴∠HEM=∠FGN；
在△EHM与△GFN中，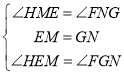
，
∴△EHM
△GFN，
∴NF=HM=AH=FC，
∴AD=AH+HD=NF+HN=HF,
在Rt△EFH中，由勾股定理知
=
,
∴AD=
=20cm．
故选：C
练习册系列答案
相关题目
【题目】铜仁某校高中一年级组建篮球队，对甲、乙两名备选同学进行定位投篮测试，每次投10个球，共投10次.甲、乙两名同学测试情况如图所示：
根据图6提供的信息填写下表：
平均数 | 众数 | 方差 | |
甲 |
| ||
乙 |
|
如果你是高一学生会文体委员，会选择哪名同学进入篮球队？请说明理由.
