题目内容
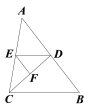
【题目】如图,在△ABC中,已知∠BDC=∠EFD,∠AED=∠ACB.
(1)试判断∠DEF与∠B的大小关系,并说明理由;
(2)若D、E、F分别是AB、AC、CD边上的中点,S△DEF=4,求S△ABC.
【答案】(1)∠DEF=∠B; (2)S△ABC=32.
【解析】
(1)由∠BDC=∠DFE,根据平行线的判定得AB∥EF,则∠ADE=∠DEF,而∠DEF=∠B,所以∠ADE=∠B,由∠AED=∠ACB可判断DE∥BC,然后根据平行线的性质得到∠ADE=∠B;故∠DEF=∠B
(2)D、E、F分别是AB、AC、CD边上的中点,根据三角形面积公式得到S△EDC =2S△DEF,S△ADC =2S△DEC,S△ABC =2S△ADC,可得S△ABC=8S△DEF进行计算即可.
(1)结论:∠DEF=∠B
证明:∵∠BDC=∠DFE,
∴AB∥EF,
∴∠ADE=∠DEF,
∵∠DEF=∠B,
∴∠AED=∠C,
∴DE∥BC,
∴∠ADE=∠B,
∴∠DEF=∠B;
(2)解:∵F为CD的中点,
∴S△DEC =2S△DEF,
同理可得:S△ADC =2S△DEC,S△ABC =2S△ADC,
∵S△DEF=4
∴S△ABC=8S△DEF=8×4=32,

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目