��Ŀ����
����Ŀ���Ķ����⣺
���θ�ʽ�ij�����Ҫ��ȥ��ĸ�еĸ��ţ��轫���ӡ���ĸͬ����һ��ǡ���Ķ��θ�ʽ��
���磺����![]() ��
��
�⣺�����ӡ���ĸͬ����![]() �ã�
�ã�![]() ��
��
���Ӧ�ã�
��1������![]() ��
��
��2������![]() ��
��
��չ���죺
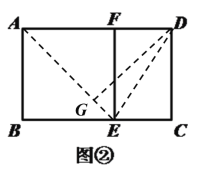
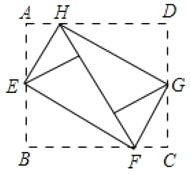
���볤�ı���![]() �ľ��νлƽ���Σ���ͼ�٣���֪�ƽ����ABCD�Ŀ�AB=1��
�ľ��νлƽ���Σ���ͼ�٣���֪�ƽ����ABCD�Ŀ�AB=1��
��1���ƽ����ABCD�ij�BC= ��
��2����ͼ�ڣ���ͼ���еĻƽ���βü���һ����ABΪ�ߵ�������ABEF���õ��µľ���DCEF���������DCEF�Ƿ�Ϊ�ƽ���Σ���֤����Ľ��ۣ�

��3����ͼ���У�����AE�����D���߶�AE�ľ���Ϊ ��
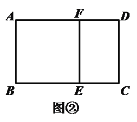
���𰸡����Ӧ�ã���1��![]() ����2��2����չ���죺��1��
����2��2����չ���죺��1��![]() ����2������DCEFΪ�ƽ���Σ����ɼ���������3��
����2������DCEFΪ�ƽ���Σ����ɼ���������3��![]()
��������
���Ӧ�ã�
��1����������еĹ��̽��м��㣻
��2����������еĹ��̽��м��㣻
��չ���죺
��1�����ݻƽ���εĶ�����AB=1���м��㣻
��2�������������AD�ij����Ӷ��ó�DF��֤��DF��EF�ı�ֵΪ![]() ���ɣ�
���ɣ�
��3������AE��DE����D��DG��AE�ڵ�G�����ݡ�AED�������ͬ�㷨�г����̣����DG�ij�����.
�⣺���Ӧ�ã�
��1����������ɵã�
![]()
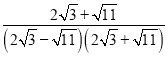 =
=![]() ��
��
��2����������ɵã�
![]()
=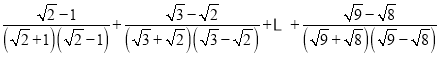
=![]()
=![]()
=2��
��չ���죺
��1���߿��볤�ı���![]() �ľ��νлƽ���Σ�
�ľ��νлƽ���Σ�
���ƽ����ABCD�Ŀ�AB=1��
��ƽ����ABCD�ij�BC=![]() =
=![]() =
=![]() ��
��
��2������DCEFΪ�ƽ���Σ������ǣ�
�ɲü���֪��AB=AF=BE=EF=CD=1��
���ݻƽ���ε����ʿɵã�AD=BC=![]() ��
��
��FD=EC=AD-AF=![]() =
=![]() ��
��
��![]() =
=![]() ��
��
�ʾ���DCEFΪ�ƽ���Σ�
��3������AE��DE����D��DG��AE�ڵ�G��
��AB=EF=1��AD=![]() ��
��
��AE=![]() ��
��
�ڡ�AED�У�
S��AED =![]() ��
��
��![]() ����
����![]() ��
��
���DG=![]() ��
��
���D���߶�AE�ľ���Ϊ![]() .
.