题目内容
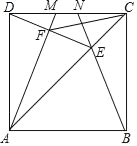
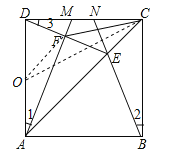
【题目】如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为4,则线段CF的最小值是_____.
【答案】2![]() ﹣2
﹣2
【解析】分析:根据正方形的性质可得AD=BC=CD,∠ADC=∠BCD,∠DCE=∠BCE,然后利用“HL”证明Rt△ADM和Rt△BCN全等,根据全等三角形对应角相等可得∠1=∠2,利用“SAS”证明△DCE和△BCE全等,根据全等三角形对应角相等可得∠2=∠3,从而得到∠1=∠3,然后求出∠AFD=90°,取AD的中点O,连接OF、OC,根据直角三角形斜边上的中线等于斜边的一半可得OF=![]() AD=2,利用勾股定理列式求出OC,然后根据三角形的三边关系可知当O、F、C三点共线时,CF的长度最小.
AD=2,利用勾股定理列式求出OC,然后根据三角形的三边关系可知当O、F、C三点共线时,CF的长度最小.
详解:在正方形ABCD中,AD=BC=CD,∠ADC=∠BCD,∠DCE=∠BCE.在Rt△ADM和Rt△BCN中,![]() ,∴Rt△ADM≌Rt△BCN(HL),∴∠1=∠2.在△DCE和△BCE中,
,∴Rt△ADM≌Rt△BCN(HL),∴∠1=∠2.在△DCE和△BCE中,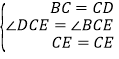 ,∴△DCE≌△BCE(SAS),∴∠2=∠3,∴∠1=∠3.
,∴△DCE≌△BCE(SAS),∴∠2=∠3,∴∠1=∠3.
∵∠ADF+∠3=∠ADC=90°,∴∠1+∠ADF=90°,∴∠AFD=180°﹣90°=90°,取AD的中点O,连接OF、OC,则OF=DO=![]() AD=2.在Rt△ODC中,OC=
AD=2.在Rt△ODC中,OC=![]() =
=![]() =2
=2![]() ,根据三角形的三边关系,OF+CF>OC,∴当O、F、C三点共线时,CF的长度最小,最小值=OC﹣OF=2
,根据三角形的三边关系,OF+CF>OC,∴当O、F、C三点共线时,CF的长度最小,最小值=OC﹣OF=2![]() ﹣2.
﹣2.
故答案为:2![]() ﹣2.
﹣2.

练习册系列答案
相关题目