题目内容
【题目】如图，等边△ABC的顶点A，B分别在函数y=-
图象的两个分支上，且AB经过原点O．当点A在函数y=-的图象上移动时，顶点C始终在函数y=
的图象上移动，则k的值为（ ）
A. 8B. 6C. 
D. 2
【答案】B
【解析】
根据反比例函数图象的对称性可得OA=OB，设OA=x，则AC=2x，OC=
x，根据等边三角形三线合一可证明△AOE∽△OCF，根据相似三角形面积比等于相似比的平方可得结论．
解：∵函数y=-
图象关于原点对称，
∴OA=OB，
连接OC，过A作AE⊥x轴于E，过C作CF⊥x轴于F，
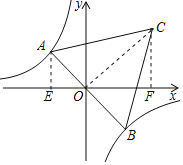
∵△ABC是等边三角形，
∴AO⊥OC，
∴∠AOC=90°，∠AOC=30°，
∴∠AOE+∠COF=90°，
设OA=x，则AC=2x，OC=x，
∵AE⊥x轴，CF⊥x轴，
∴∠AEO=∠OFC=∠AOE+∠OAE=90°，
∴∠COF=∠OAE，
∴△AOE∽△OCF，
∴
=
=
=
，
∵顶点A在函数y=-图象的分支上，
∴S△AOE=1，
∴S△OCF=3，
∵顶点C始终在函数y=
的图象上，
∴k=6，
故选：B．
【题目】下表是在汛期中防汛指挥部对某河流做的一星期的水位测量（单位：
）
（注：此河流的警戒水位为
，“+”表示比河流的警戒水位高，“-”表示比河流的警戒水位低）
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位记录 | +2.3 | +0.7 | -5.0 | -1.5 | +3.6 | +1.0 | -2.5 |
（1）本周河流水位最高的一天是______，最低的一天是______，这两天的实际水位分别是_______；
（2）完成下列本周的水位变化表（单位：），（已知上周末河流的水位比警戒水位低
.注：规定水位比前一天上升用“+”，比前一天下降用“-”，不升不降用“0”）
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化 |
（3）与上周末相比，本周末河流水位上升了还是下降了？变化了多少？
