题目内容
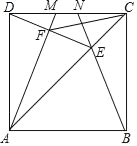
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,AE平分∠CAB交CD于点F,交BC于点E,EH⊥AB,垂足为H,连接FH.
(1)求证:CF=CE
(2)试判断四边形CFHE的形状,并说明理由.

【答案】(1)证明见解析;(2)四边形CFHE是菱形.
【解析】
(1)如图,先由直角三角形的性质证∠3=∠5,再由对顶角相等和等量代换得∠4=∠5,从而得到CF=CE;
(2)由角平分线的性质定理得CE=EH,又因为CF=CE,所以CF=EH,再证CF∥EH,得平行四边形CFHE,又因为CF=CE,四边形CFHE是菱形.
(1)证明:如图
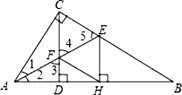
∵∠ACB=90°,CD⊥AB垂足为D,
∴∠1+∠5=90°,∠2+∠3=90°,
又∵∠AE平分∠CAB,
∴∠1=∠2,
∴∠3=∠5,
∵∠3=∠4,
∴∠4=∠5,
∴CF=CE
(2)四边形CFHE是菱形
理由:∵AE平分∠CAB,CE⊥AC,EH⊥AB,
∴CE=EH,
由(1)CF=CE,
∴CF=EH,
∵CD⊥AB,EH⊥AB,
∴∠CDB=90°,∠EHB=90°,
∴∠CDB=∠EB,
∴CD∥EH,即CF∥EH,
∴四边形CFHE是平行四边形.
∵CF=CE,
∴四边形CFHE是菱形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】下表是在汛期中防汛指挥部对某河流做的一星期的水位测量(单位:![]() )
)
(注:此河流的警戒水位为![]() ,“+”表示比河流的警戒水位高,“-”表示比河流的警戒水位低)
,“+”表示比河流的警戒水位高,“-”表示比河流的警戒水位低)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位记录 | +2.3 | +0.7 | -5.0 | -1.5 | +3.6 | +1.0 | -2.5 |
(1)本周河流水位最高的一天是______,最低的一天是______,这两天的实际水位分别是_______;
(2)完成下列本周的水位变化表(单位:![]() ),(已知上周末河流的水位比警戒水位低
),(已知上周末河流的水位比警戒水位低![]() .注:规定水位比前一天上升用“+”,比前一天下降用“-”,不升不降用“0”)
.注:规定水位比前一天上升用“+”,比前一天下降用“-”,不升不降用“0”)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化 |
(3)与上周末相比,本周末河流水位上升了还是下降了?变化了多少?