Question

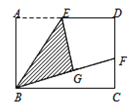
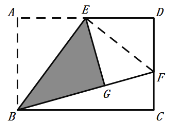
【题目】如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠 得到△GBE，且点G在矩形ABCD内部．将BG延长交DC 于点F，若DC=nDF，则 =______．

Answer 1

【答案】

【解析】

连接EF，就可以得出△EGF≌△EDF，就有GF=DF，设DF=，BC=，则有GF=，AD=，进而可以表示出CF、BF，在Rt△BCF中由勾股定理建立等式就可以求出结论．

连接EF，则∠EGF=∠D=90°．

∵点E是AD的中点，

∴由折叠的性质知，EG=ED

在Rt△EGF和Rt△EDF中

∴Rt△EGF≌Rt△EDF（HL）．

∴GF=DF；

设DF=，BC=，则有GF=，AD=．

∵DC=DF，

∴DC=AB=BG=，CF=，

∴BF=BG+GF=．

在Rt△BCF中，由勾股定理得：

，即．

化简得：

∴

故答案为：