Question

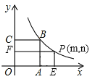
【题目】如图，在平面直角坐标系中，点A、C的坐标分别为（0，8）、（6，0），以AC为直径作⊙O，交坐标轴于点B，点D是⊙O 上一点，且，过点D作DE⊥BC，垂足为E．

（1）求证：CD平分∠ACE；

（2）判断直线ED与⊙O的位置关系，并说明理由；

（3）求线段CE的长．

Answer 1

【答案】（1）见解析；（2）直线ED与⊙O相切，理由见解析；（3）2

【解析】

(1)说明∠DCE=∠DAB, ∠DAB=∠ACD,从而说明CD平分∠ACE；（2）连接OD，利用∠EDC+∠DCE=90°,∠DCE=∠ACD=∠ODC，从而∠EDC+∠ODC=90°；（3）延长DO交AB于点H，求出BD的长，即BE的长，CE=BE-BC.

（1）∵四边形ABCD是⊙O内接四边形，∴∠BAD+∠BCD=180°，

又∵∠BCD+∠DCE=180°， ∴∠DCE=∠BAD，

∵＝， ∴∠BAD=∠ACD，

∴∠DCE=∠ACD， ∴CD平分∠ACE．

（2）直线ED与⊙O相切．连接OD．

∵OC=OD，∴∠ODC=∠OCD，

又∵∠DCE=∠ACD，∴∠DCE=∠ODC，

∴OD∥BE，∴∠ODE=∠DEC，

又∵DE⊥BC，∴∠DEC=90°，

∴∠ODE=90° ∴OD⊥DE，

∴ED与⊙O相切．

（3）延长DO交AB于点H．

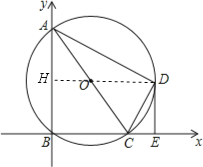∵OD∥BE，O是AC的中点， ∴H是AB的中点，

∴HO是△ABC的中位线，

∴HO=BC=3，

又∵AC为直径， ∴∠ADC=90°，

又∵O是AC的中点

∴OD=AC=×=5，

∴HD=3+5=8，

∵∠ABC=∠DEC=∠ODE=90°，

∴四边形BEDH是矩形，

∴BE=HD=8，

∴CE=8﹣6=2．