题目内容
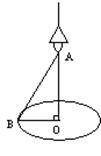
如图,在一张圆桌(圆心为点O)的正上方点A处吊着一盏照明灯,实践证明:桌子边沿处的光的亮度与灯距离桌面的高度AO有关,且当sin∠ABO=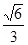 时,桌子边沿处点B的光的亮度最大,设OB=60cm,求此时灯距离桌面的高度OA(结果精确到1cm).
时,桌子边沿处点B的光的亮度最大,设OB=60cm,求此时灯距离桌面的高度OA(结果精确到1cm).
(参考数据: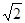 ≈1.414;
≈1.414;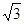 ≈1.732;
≈1.732;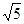 ≈2.236)
≈2.236)
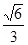 时,桌子边沿处点B的光的亮度最大,设OB=60cm,求此时灯距离桌面的高度OA(结果精确到1cm).
时,桌子边沿处点B的光的亮度最大,设OB=60cm,求此时灯距离桌面的高度OA(结果精确到1cm).(参考数据:
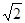 ≈1.414;
≈1.414;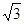 ≈1.732;
≈1.732;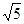 ≈2.236)
≈2.236)
解法一:在Rt△OAB中,
∵sin∠ABO=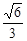 ,∴
,∴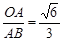
即OA=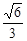 AB
AB
又OA2+OB2=AB2,且OB=60cm
解得OA=60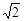 ≈85cm
≈85cm
答:高度OA约为85cm
解法二:∵OA⊥OB,sin∠ABO=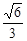
∴ 可设OA=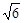 x ,AB="3" x(x>0)
x ,AB="3" x(x>0)
∵OA2+OB2=AB2,∴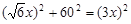
解得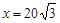
∴OA=60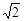 ≈85cm
≈85cm
答:高度OA约为85cm
例①先求cos∠ABO,再求tan∠ABO;②由sin∠ABO=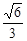 ,设OA=
,设OA=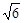 x ,AB="3" x(x>0),得BO=
x ,AB="3" x(x>0),得BO=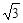 x=60等。
x=60等。
∵sin∠ABO=
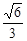 ,∴
,∴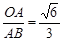
即OA=
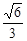 AB
AB又OA2+OB2=AB2,且OB=60cm
解得OA=60
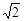 ≈85cm
≈85cm答:高度OA约为85cm
解法二:∵OA⊥OB,sin∠ABO=
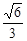
∴ 可设OA=
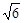 x ,AB="3" x(x>0)
x ,AB="3" x(x>0)∵OA2+OB2=AB2,∴
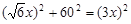
解得
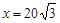
∴OA=60
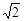 ≈85cm
≈85cm 答:高度OA约为85cm
例①先求cos∠ABO,再求tan∠ABO;②由sin∠ABO=
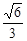 ,设OA=
,设OA=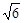 x ,AB="3" x(x>0),得BO=
x ,AB="3" x(x>0),得BO=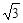 x=60等。
x=60等。解法一:在直角三角形ABO中,sin∠ABO=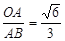 ,所以
,所以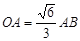 ,然后根据勾股定理得
,然后根据勾股定理得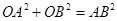 ,且OB=60cm解得OA;
,且OB=60cm解得OA;
解法二:同解法一类似,只不过少了OA、OB之间的转化,而是根据sin∠ABO=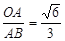 ,分别假设
,分别假设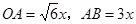 ,再有OB=60,根据勾股定理先求出x,再进而求出OA的长.
,再有OB=60,根据勾股定理先求出x,再进而求出OA的长.
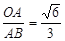 ,所以
,所以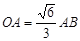 ,然后根据勾股定理得
,然后根据勾股定理得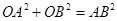 ,且OB=60cm解得OA;
,且OB=60cm解得OA;解法二:同解法一类似,只不过少了OA、OB之间的转化,而是根据sin∠ABO=
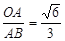 ,分别假设
,分别假设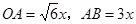 ,再有OB=60,根据勾股定理先求出x,再进而求出OA的长.
,再有OB=60,根据勾股定理先求出x,再进而求出OA的长.
练习册系列答案
相关题目
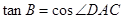 ,
,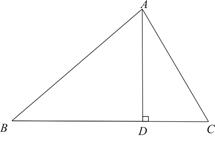
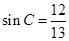 ,BC=12,求AD的长.
,BC=12,求AD的长. 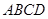 中,以点
中,以点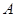 为圆心,
为圆心,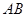 为半径的圆,交
为半径的圆,交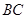 于点
于点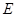 .
.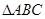 ≌
≌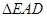 ;
;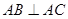 ,
,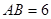 ,
,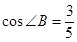 ,求
,求 的长.
的长.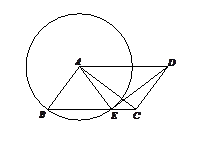
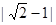 +2sin45°
+2sin45°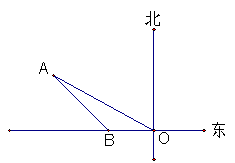
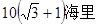
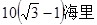
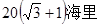
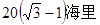

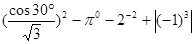 .
.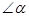 的补角是120°,则
的补角是120°,则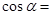 。
。