ƒøƒ⁄»ð
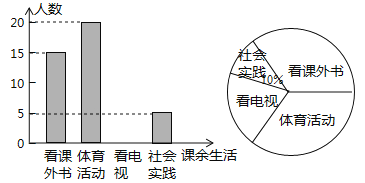
°æƒø°øŒ™¡ÀΩ‚ƒ≥÷–—ß—ß…˙øŒ”ý…˙ªÓ«Èøˆ£¨∂‘œ≤∞Æø¥øŒÕ‚ È°¢Ã”˝ªÓ∂Ø°¢ø¥µÁ ”°¢…Áª· µº˘Àƒ∏ˆ∑Ω√ʵƒ»À ˝Ω¯––µ˜≤ÈÕ≥º∆£¨œ÷¥”∏√–£Àʪ˙≥È»°n√˚—ß…˙◊˜Œ™—˘±æ£¨≤…”√Œ æ̵˜≤ȵƒ∑Ω Ω ’ºØ ˝æð£®≤Œ”ÎŒ æ̵˜≤ȵƒ√ø√˚—ß…˙÷ªƒÐ—°‘Ò∆‰÷–“ªœÓ£©.≤¢∏˘æðµ˜≤ȵ√µΩµƒ ˝æðªÊ÷∆≥…¡À»ÁÕºÀ˘ 浃¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£¨”…Õº÷–Ã·π©µƒ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
£®1£©«Î÷±Ω”≤π»´Ãı–ŒÕ≥º∆Õº£ª
£®2£©»Ù∏√–£π≤”–—ß…˙3200√˚£¨ ‘π¿º∆∏√–£œ≤∞Æø¥øŒÕ‚ ȵƒ—ß…˙»À ˝°£
£®3£©»Ù±ªµ˜≤Èœ≤∞ÆÔ˝ªÓ∂صƒ4√˚—ß…˙÷–”–3√˚ƒ–…˙∫Õ1√˚≈Æ…˙£¨œ÷¥”’‚4√˚—ß…˙÷–»Œ“‚≥È»°2√˚£¨«Î”√¡–±ÌªÚª≠ ˜◊¥Õºµƒ∑Ω∑®«Û«°∫√≥È2√˚ƒ–…˙µƒ∏≈¬ .
°æ¥∞∏°ø£®1£©ø¥µÁ ”µƒ—ß…˙”–10»À£®Õº¬‘£©£ª£®2£©‘º”–960»À∞Æø¥øŒÕ‚ È£ª£®3£©∏≈¬ Œ™![]() £®π˝≥ú˚Ω‚Œˆ£©
£®π˝≥ú˚Ω‚Œˆ£©
°æΩ‚Œˆ°ø
1£©œ»”√œ≤∞Æ…Áª· µº˘µƒ»À ˝≥˝“‘À¸À˘’ºµƒ∞Ÿ∑÷±»º∆À„≥ˆµ˜≤ȵƒ◊лÀ ˝£¨‘Ÿº∆À„≥ˆø¥µÁ ”µƒ»À ˝£¨»ª∫Û≤π»´Ãı–ŒÕ≥º∆Õº£ª
£®2£©”√3200≥À“‘—˘±æ÷–œ≤∞Æø¥øŒÕ‚ È»À ˝µƒ∞Ÿ∑÷±»ø…π¿º∆∏√–£œ≤∞Æø¥øŒÕ‚ ȵƒ—ß»À ˝£ª
£®3£©ª≠ ˜◊¥Õº’π æÀ˘”–12÷÷µ»ø…ƒÐµƒΩ·π˚ ˝£¨‘Ÿ’“≥ˆ«°∫√≥ȵΩ2√˚ƒ–µƒΩ·π˚ ˝£¨»ª∫Û∏˘æð∏≈¬ π´ Ωº∆À„£Æ
Ω‚£∫£®1£©µ˜≤ȵƒ◊лÀ ˝Œ™5°¬10%=50£®»À£©£¨
À˘“‘ø¥µÁ ”µƒ»À ˝Œ™50-15-20-5=10£®»À£©£¨
≤π»´Ãı–ŒÕ≥º∆ÕºŒ™£∫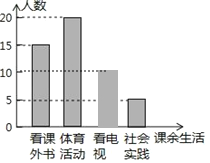
£®2£©3200°¡![]() =960£¨
=960£¨
À˘“‘π¿º∆∏√–£œ≤∞Æø¥øŒÕ‚ ȵƒ—ß»À ˝Œ™960»À£ª
£®3£©ª≠ ˜◊¥Õº£∫
π≤”–12÷÷µ»ø…ƒÐµƒΩ·π˚ ˝£¨∆‰÷–«°∫√≥ȵΩ2√˚ƒ–µƒΩ·π˚ ˝Œ™6£¨
À˘“‘«°∫√≥ȵΩ2√˚ƒ–µƒ∏≈¬ =![]() =
=![]() £Æ
£Æ

 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏