题目内容
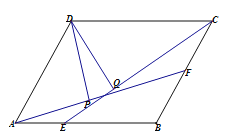
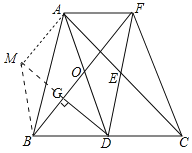
【题目】如图,在△ABC中,点D,E分别是边BC,AC上的中点,连接DE,并延长DE至点F,使EF=ED,连接AD,AF,BF,CF,线段AD与BF相交于点O,过点D作DG⊥BF,垂足为点G.
(1)求证:四边形ABDF是平行四边形;
(2)当![]() 时,试判断四边形ADCF的形状,并说明理由;
时,试判断四边形ADCF的形状,并说明理由;
(3)若∠CBF=2∠ABF,求证:AF=2OG.

【答案】(1)证明见解析;(2)四边形ADCF是矩形,理由见解析;(3)证明见解析.
【解析】
(1)欲证明四边形ABDF是平行四边形,只要证明AF∥BD,AF=BD即可.
(2)结论:四边形ADCF是矩形,只要证明∠DAF=90°即可.
(3)作AM⊥DG 于M,连接BM,先证明AM=2OG,再证明AM=AF即可解决问题.
(1)证明:∵点D,E分别是边BC,AC上的中点,
∴ED∥AB,AE=CE,
∵EF=ED,
∴四边形ADCF是平行四边形,
∴AF∥BC,
∴四边形ABDF是平行四边形;
(2)四边形ADCF是矩形.
理由:∵AE=![]() DF,EF=ED,
DF,EF=ED,
∴AE=EF=DE,
∴∠EAF=∠AFE,∠DAE=∠ADE,
∴∠DAF=∠EAF+∠EAD=![]() ×180°=90°,
×180°=90°,
由(1)知:四边形ADCF是平行四边形;
∴四边形ADCF是矩形;
(3)证明:作AM⊥DG 于M,连接BM.
∵四边形ABDF是平行四边形,
∴OA=OD,∵OG∥AM,
∴GM=GD,
∴AM=2OG,
∵BG⊥DM,GM=GD,
∴BM=BD,
∴∠CBF=∠MBG,
∵∠CBF=2∠ABF,
∴∠ABM=∠ABF,
∵AM∥BF,
∴∠MAB=∠ABF,
∴∠MAB=∠MBA,
∴AM=BM=BD=AF=2OG,
∴AF=2OG.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案【题目】某学校计划组织全校1500名师生外出参加集体活动.经过研究,决定租用当地租车公司一共60辆![]() 、
、![]() 两种型号客车作为交通工具.
两种型号客车作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人 | 400元 |
| 20人 | 300元 |
注:载客量指的是每辆客车最多可载该校师生的人数.
学校租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式,请直接写出
的函数解析式,请直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过22000元,一共有几种租车方案?并结合函数性质说明哪种租车方案最省钱?