题目内容
【题目】如图,已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.求∠DCE的大小.
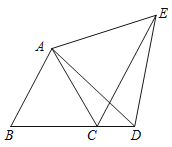
【答案】60°
【解析】
由△ABC和△ADE是等边三角形可以得出AB=BC=AC,AD=AE,∠ABC=∠ACB=∠BAC=∠DAE=60°,得出∠ABD=60°,再证明△ABD≌△ACE,得出∠ABD=∠ACE=60°,即可得出结论.
∵△ABC和△ADE是等边三角形,
∴∠DAE=∠BAC=∠ABC=∠ACB=60°,AB=AC,AD=AE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
在△ABD和△ACE中,
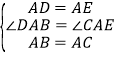 ,
,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠ABC=60°.
∴∠DCE=180°-∠ACE-∠ACB=180°-60°-60°=60°.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目