Question

【题目】 已知矩形纸片ABCD中，AB＝4，BC＝6

操作将矩形纸片沿EF折叠使点B落在边CD上．探究

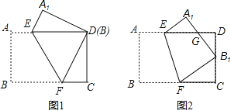
（1）如图1，若点B与点D重合，你认为△EDA1和△FDC全等吗？如果全等，请给出证明；如果不全等，请说明理由；

（2）如图2，CD上是否存在一点B1，当点B落在B1处时，△FCB1与△B1DG全等？若存在，求出B1C的长度；若不存在，说明理由．

Answer 1

【答案】（1）全等，证明见解析；（2）存在，.

【解析】

（1）由四边形ABCD是矩形，可得∠A=∠B=∠C=∠ADC=90°，AB=CD，由折叠的性质可得：∠A=∠A1，∠B=∠A1DF=90°，CD=A1D，然后利用同角的余角相等，可证得∠A1DE=∠CDF，则可利用ASA证得△EDA1和△FDC全等；
（2）设B1C=a，则有FC=B1D=4-a，B1F=BF=2+a，在直角△FCB1中，可得（2+a）2=（4-a）2+a2，解此方程即可求得答案．

解：（1）全等．

证明：∵四边形ABCD是矩形，

∴∠A＝∠B＝∠C＝∠ADC＝90°，AB＝CD，

由题意知：∠A＝∠A1，∠B＝∠A1DF＝90°，AB=CD＝A1D，∠B＝∠A1DF＝90°

∴∠A1＝∠C＝90°，∠CDF+∠EDF＝90°，∠EDA1+∠EDF＝90°

∴∠A1DE＝∠CDF，

在△EDA1和△FDC中，

，

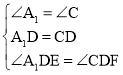∴△EDA1≌△FDC（ASA）；

（2）∵△FCB1与△B1DG全等，∠CFB1＝∠GB1D，

∴CF＝DB1，

设B1C＝a，则有FC＝B1D＝4﹣a，B1F＝BF＝2+a，

在直角△FCB1中，可得（2+a）2＝（4﹣a）2+a2，

整理得a2﹣12a+12＝0，

解得：a＝6﹣2（另一解舍去），

∴当B1C＝6﹣2时，△FCB1与△B1DG全等．