题目内容
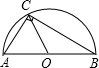
以线段AB为直径作一个半圆,圆心为O,C是半圆周上的点,且OC2=AC•BC,则∠CAB=______.
∵AB为直径,C是半圆周上的点,
∴∠ACB=90°,0A=OB=OC,
∴S△ABC=
AC•BC,
S△AOC=
S△ABC;
又∵OC2=AC•BC,
∴
OC2=2•
OC2sin∠AOC,
∴sin∠AOC=
;
当∠AOC=30°时,∠COB=180°-30°=150°
∠CAB=
∠COB=75°(同弧所对的圆周角是圆心角的一半);
当∠AOC=150°时,∠COB=180°-150°=30°
∠CAB=
∠COB=15°(同弧所对的圆周角是圆心角的一半).
故答案为:75°或15°.
∴∠ACB=90°,0A=OB=OC,
∴S△ABC=
| 1 |
| 2 |
S△AOC=
| 1 |
| 2 |
又∵OC2=AC•BC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴sin∠AOC=
| 1 |
| 2 |
当∠AOC=30°时,∠COB=180°-30°=150°
∠CAB=
| 1 |
| 2 |
当∠AOC=150°时,∠COB=180°-150°=30°
∠CAB=
| 1 |
| 2 |
故答案为:75°或15°.


练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目