题目内容
等腰梯形ABCD中，AD∥BC，求证：A，B，C，D四个顶点共圆．
证明：如图：
∵ABCD是等腰梯形，且AD∥BC，
∴∠A=∠D，∠B=∠C，∠A+∠B=180°．
∴∠A+∠C=∠B+∠D=180°．
根据对角互补的四边形是圆的内接四边形，
所以A，B，C，D四点共圆．
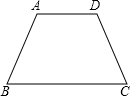
∵ABCD是等腰梯形，且AD∥BC，
∴∠A=∠D，∠B=∠C，∠A+∠B=180°．
∴∠A+∠C=∠B+∠D=180°．
根据对角互补的四边形是圆的内接四边形，
所以A，B，C，D四点共圆．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
