题目内容
在△ABC中,AD是△ABC的角平分线.
(1)如图1,过C作CE∥AD交BA延长线于点E,若F为CE的中点,连结AF,求证:AF⊥AD;
(2)如图2,M为BC的中点,过M作MN∥AD交AC于点N,若AB=4, AC=7,
求NC的长.
(1)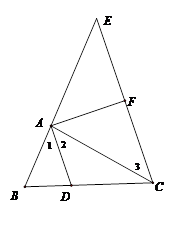
∵AD为△ABC的角平分线,∴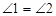 ,∵CE∥AD,∴
,∵CE∥AD,∴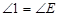 ,
,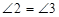 ,∴
,∴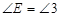 ,∴AC=AE,∵F为EC的中点,∴AF⊥BC,∴
,∴AC=AE,∵F为EC的中点,∴AF⊥BC,∴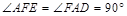 ,∴AF⊥AD。
,∴AF⊥AD。
(2)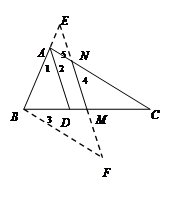
CN=5.5
解析试题分析:(1)由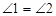 与CE∥AD,可以通过两直线平行性质推出内错角和同位角相等,等量代换得出
与CE∥AD,可以通过两直线平行性质推出内错角和同位角相等,等量代换得出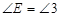 ,又等腰三角形底边的中线与底边上的高是同一条线,所以得出AF⊥BC,由此AF⊥AD。
,又等腰三角形底边的中线与底边上的高是同一条线,所以得出AF⊥BC,由此AF⊥AD。
(2)延长BA与MN延长线于点E,过B作BF∥AC交NM延长线于点F,∴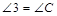 ,
,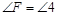 ,∵M为BC的中点,∴BM=CM,在△BFM和△CNM中,
,∵M为BC的中点,∴BM=CM,在△BFM和△CNM中,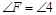 ,
,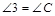 ,
,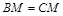 ,∴△BFM≌△CNM,∴BF=CN,∵MN∥AD,∴
,∴△BFM≌△CNM,∴BF=CN,∵MN∥AD,∴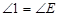 ,
,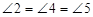 ,∴
,∴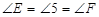 ,∴
,∴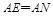 ,
,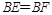 ,设
,设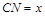 ,则
,则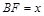 ,
,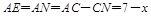 ,
,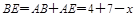 ,∴4+7-x=x,解得 x=5.5,∴CN=5.5
,∴4+7-x=x,解得 x=5.5,∴CN=5.5
考点:两平行线与交线的性质,等腰三角形三线合一
点评:本题考查的是学生对两平行线与过这两条线的直线相交的性质;等腰三角形的三线合一很重要,通过求出其中任意一个数据,即可知道其他两个的数据;第二问关键在于做辅助线,辅助线在几何题中也是十分常用的一种方法。

练习册系列答案
相关题目
 在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上.若BC=8cm,AD=6cm,且PN=2PQ,求矩形PQMN的周长.
在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上.若BC=8cm,AD=6cm,且PN=2PQ,求矩形PQMN的周长.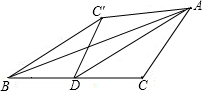 如图,在△ABC中,AD是BC上的中线,BC=4,∠ADC=30°,把△ADC沿AD所在直线翻折后点C落在点C′的位置,那么点D到直线BC′的距离是
如图,在△ABC中,AD是BC上的中线,BC=4,∠ADC=30°,把△ADC沿AD所在直线翻折后点C落在点C′的位置,那么点D到直线BC′的距离是
 (2013•温州二模)如图,在△ABC中,AD是它的角平分线,∠C=90°,E在AB边上,以AE为直径的⊙O交BC于点D,交AC于点F.
(2013•温州二模)如图,在△ABC中,AD是它的角平分线,∠C=90°,E在AB边上,以AE为直径的⊙O交BC于点D,交AC于点F. 如图,在△ABC中,AD是∠BAC的平分线,DE、DF分别是△ABD和△ACD的高线,求证:AD⊥EF.
如图,在△ABC中,AD是∠BAC的平分线,DE、DF分别是△ABD和△ACD的高线,求证:AD⊥EF.