题目内容
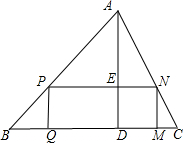在△ABC中，AD是高，矩形PQMN的顶点P、N分别在AB、AC上，QM在边BC上．若BC=8cm，AD=6cm，且PN=2PQ，求矩形PQMN的周长．
分析：由题意可得出PQ：AD=BP：AB，PN：BC=AP：AB，BC=8，AD=6，据此可得出PQ，PN的值，故可得出矩形PQMN的周长．
解答：解：由题意得；PQ：AD=BP：AB，PN：BC=AP：AB
∴
+
=
+
=
=
=1，
又∵PN=2PQ，BC=8cm，AD=6cm，
∴
+
=1，
∴PQ=2.4
则PN=4.8，
∴矩形PQMN的周长=14.4cm．
∴
| PQ |
| AD |
| PN |
| BC |
| BP |
| AB |
| AP |
| AB |
| AP+PB |
| AB |
| AB |
| AB |
又∵PN=2PQ，BC=8cm，AD=6cm，
∴
| PQ |
| 6 |
| 2PQ |
| 8 |
∴PQ=2.4
则PN=4.8，
∴矩形PQMN的周长=14.4cm．
点评：本题考查了相似三角形的性质，能够灵活运用比例线段解决本题的关键，技巧性很强，要注意掌握做题技巧性．
练习册系列答案
名校课堂系列答案
相关题目
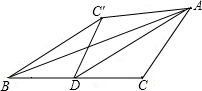如图，在△ABC中，AD是BC上的中线，BC=4，∠ADC=30°，把△ADC沿AD所在直线翻折后点C落在点C′的位置，那么点D到直线BC′的距离是
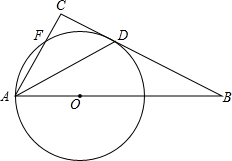（2013•温州二模）如图，在△ABC中，AD是它的角平分线，∠C=90°，E在AB边上，以AE为直径的⊙O交BC于点D，交AC于点F．
如图，在△ABC中，AD是∠BAC的平分线，DE、DF分别是△ABD和△ACD的高线，求证：AD⊥EF．