题目内容
 (2013•温州二模)如图,在△ABC中,AD是它的角平分线,∠C=90°,E在AB边上,以AE为直径的⊙O交BC于点D,交AC于点F.
(2013•温州二模)如图,在△ABC中,AD是它的角平分线,∠C=90°,E在AB边上,以AE为直径的⊙O交BC于点D,交AC于点F.(1)求证:BC是⊙O的切线;
(2)已知∠B=30°,AD的弦心距为1,求AF的长.
分析:(1)如图,连接OD.欲证明BC是⊙O的切线,只需证得OD⊥BC;
(2)如图,过圆心O作OE⊥AD于点E,则OE=1.根据垂径定理求得AD=2AE.通过解直角△ACD求得CD、AC的长度.然后利用切割线定理来求CF=1,则AF=AC-CF=2.
(2)如图,过圆心O作OE⊥AD于点E,则OE=1.根据垂径定理求得AD=2AE.通过解直角△ACD求得CD、AC的长度.然后利用切割线定理来求CF=1,则AF=AC-CF=2.
解答: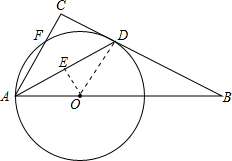 (1)证明:连结OD.
(1)证明:连结OD.
∵AD平分∠CAB,
∴∠CAD=∠DAB.
∵OA=OD,
∴∠DAB=∠ADO,
∴∠CAD=∠ADO,
∴AC∥DO,
∴∠ODB=∠C=90°,即OD⊥BC.
又∵OD是⊙O的半径,
∴BC是圆O的切线;
(2)如图,过圆心O作OE⊥AD于点E,则OE=1.
∵∠C=90°,∠B=30°,
∴∠CAB=60°.
由(1)知,∠CAD=∠DAB,
∴∠CAD=∠DAB=30°.
在直角△AEO中,AE=OE•cot30°=
,则根据垂径定理知AD=2AE=2
.
在直角△ACD中,CD=
AD=AE=
,AC=CD•cot30°=3,
∵CD是⊙O的切线,
∴CD2=CF•AC,则CF=1,
∴AF=AC-CF=2,即AF的长度是2.
 (1)证明:连结OD.
(1)证明:连结OD.∵AD平分∠CAB,
∴∠CAD=∠DAB.
∵OA=OD,
∴∠DAB=∠ADO,
∴∠CAD=∠ADO,
∴AC∥DO,
∴∠ODB=∠C=90°,即OD⊥BC.
又∵OD是⊙O的半径,
∴BC是圆O的切线;
(2)如图,过圆心O作OE⊥AD于点E,则OE=1.
∵∠C=90°,∠B=30°,
∴∠CAB=60°.
由(1)知,∠CAD=∠DAB,
∴∠CAD=∠DAB=30°.
在直角△AEO中,AE=OE•cot30°=
| 3 |
| 3 |
在直角△ACD中,CD=
| 1 |
| 2 |
| 3 |
∵CD是⊙O的切线,
∴CD2=CF•AC,则CF=1,
∴AF=AC-CF=2,即AF的长度是2.
点评:本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 (2013•温州二模)如图,圆锥的底面半径为3cm,高为4cm,那么这个圆锥的侧面积是
(2013•温州二模)如图,圆锥的底面半径为3cm,高为4cm,那么这个圆锥的侧面积是 (2013•温州二模)如图是由5个大小相同的正方体组成的几何体,它的左视图是( )
(2013•温州二模)如图是由5个大小相同的正方体组成的几何体,它的左视图是( )