题目内容
【题目】如图,已知![]() 是反比例函数
是反比例函数![]() 图象上的两点,
图象上的两点,![]() 轴,交
轴,交![]() 轴于点
轴于点![]() .动点
.动点![]() 从坐标原点
从坐标原点![]() 出发,沿
出发,沿![]() 匀速运动,终点为
匀速运动,终点为![]() .过点
.过点![]() 作
作![]() 轴于
轴于![]() .设
.设![]() 的面积为
的面积为![]() 点
点![]() 运动的时间为
运动的时间为![]() 则
则![]() 关于
关于![]() 的函数图象大致为( )
的函数图象大致为( )

A.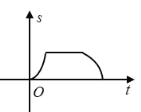 B.
B.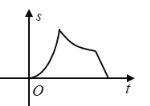
C. D.
D.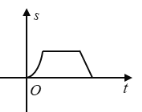
【答案】D
【解析】
点P在OA上运动时,S与t成二次函数关系;②点P在AB上运动时,此时△OPQ的面积不变;③点P在BC上运动时,S减小,S与t的关系为一次函数,从而进行排除,即可得到答案.
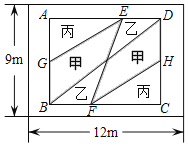
解:解:①当点P在线段OA上运动时,设P(x,y),则面积可表示为S=ax2(a是大于0的常数,x>0),图象为抛物线的一部分,排除C;
②当点P在AB上运动时,此时△OPQ的面积S=![]() ,是定值,排除B;
,是定值,排除B;
③点P在BC上运动时,则S=![]() OC×PC,OC为定值,因为
OC×PC,OC为定值,因为![]() 沿
沿![]() 是匀速运动,所以S与t成一次函数关系.故排除A.
是匀速运动,所以S与t成一次函数关系.故排除A.
故选D.

【题目】对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度与华氏温度之间是一次函数关系.如图所示是一个家用温度表的表盘、其左边为摄氏温度的刻度和读数(单位![]() ),右边为华氏温度的刻度和读数(单位
),右边为华氏温度的刻度和读数(单位![]() ).从温度计的刻度上可以看出,摄氏温度
).从温度计的刻度上可以看出,摄氏温度![]() 与华氏温度
与华氏温度![]() 部分对应关系如下表:
部分对应关系如下表:
| ··· |
|
| ··· |
| ··· |
|
| ··· |

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当摄氏温度为零下![]() 时,求华氏温度为多少?
时,求华氏温度为多少?
【题目】《郑州市城市生活垃圾分类管理办法》于2019年12月起施行,某社区要投放![]() 两种垃圾桶,负责人小李调查发现:
两种垃圾桶,负责人小李调查发现:
购买数量少于 | 购买数量不少于 | |
| 原价销售 | 以原价的 |
| 原价销售 | 以原价的 |
若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需要付款
个,则共需要付款![]() 元;若购买
元;若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需付款
个,则共需付款![]() 元.
元.
(1)求![]() 两种垃圾桶的单价各为多少元?
两种垃圾桶的单价各为多少元?
(2)若需要购买![]() 两种垃圾桶共
两种垃圾桶共![]() 个,且
个,且![]() 种垃圾桶不多于
种垃圾桶不多于![]() 种垃圾桶数量的
种垃圾桶数量的![]() ,如何购买使花费最少?最少费用为多少元?请说明理由.
,如何购买使花费最少?最少费用为多少元?请说明理由.