Question

【题目】已知：抛物线y＝x2﹣2（m﹣1）x﹣1﹣m

（1）当m＝2时，求该抛物线的对称轴和顶点坐标；

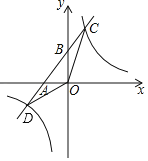
（2）设该抛物线与x轴交于A（x1，0）、B（x2，0），x1＜0＜x2，与y轴交于点C，且满足，求这个抛物线的解析式；

（3）在（2）的条件下，是否存在着直线y＝kx+b与抛物线交于点P、Q，使y轴平分△CPQ的面积？若存在，求出k，b应满足的条件；若不存在，请说明理由．

Answer 1

【答案】（1）对称轴直线为x＝1，顶点坐标为（1，﹣4）；（2）y＝x2﹣2x﹣3；（3）存在，当k＝﹣2且b＞﹣3时直线y＝kx+b与抛物线交于点P，Q使y轴平分△CPQ的面积．

【解析】

（1）将m＝2代入抛物线解析式中，并且配方得出y＝x2﹣2x﹣3＝（x﹣1）2﹣4，即可得出结论；

（2）先表示出AO＝﹣x1，OB＝x2，CO＝m+1＞0，再用 ，建立方程化简得出（m+1）（x1+x2）＝﹣2x1x2，再根据根与系数的关系得出x1+x2＝2（m﹣1），x1x2＝﹣（1+m），即可得出结论；

（3）设点P的横坐标为xP，点Q的横坐标为xQ，直线与y轴交于点E，利用面积相等得出|xP|＝|xQ|，即xP＝﹣xQ，再由，得出x2﹣（k+2）x﹣（b+3）＝0，进而得出xP+xQ＝k+2＝0，即可得出结论．

（1）当m＝2时，得出y＝x2﹣2x﹣3＝（x﹣1）2﹣4，

∴抛物线的对称轴直线为x＝1，顶点坐标为（1，﹣4）；

（2）∵x1＜0＜x2，

∴AO＝﹣x1，OB＝x2，

又∵a＝1＞0，

∴CO＝m+1＞0，

∴m＞﹣1，

∵，

∴CO（OB﹣AO）＝2AOOB，

即（m+1）（x1+x2）＝﹣2x1x2

对于抛物线y＝x2﹣2（m﹣1）x﹣1﹣m，

令y＝0，则0＝x2﹣2（m﹣1）x﹣1﹣m，

∵x1+x2＝2（m﹣1），x1x2＝﹣（1+m），

∴（m+1）2（m﹣1）＝2（1+m），

解得m＝﹣1（舍去），m＝2．

∴二次函数的解析式为y＝x2﹣2x﹣3．

（3）存在着直线y＝kx+b与抛物线交于点P、Q，使y轴平分△CPQ的面积，

设点P的横坐标为xP，点Q的横坐标为xQ，直线与y轴交于点E，

∵S△PCE＝S△QCE，CE|xP|＝CE|xQ|，

∴|xP|＝|xQ|，

∵y轴平分△CPQ的面积，

∴点P、Q在y轴异侧，

即xP＝﹣xQ，

由，

得x2﹣（k+2）x﹣（b+3）＝0

而xP，xQ为x2﹣（k+2）x﹣（b+3）＝0的两根，

∴xP+xQ＝k+2＝0，

∴k＝﹣2，

又∵直线与抛物线有两个交点，

∴b+3＞0，即b＞﹣3，

∴当k＝﹣2且b＞﹣3时直线y＝kx+b与抛物线交于点P，Q使y轴平分△CPQ的面积.