题目内容
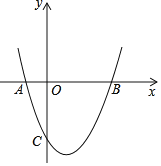
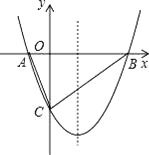
【题目】如图,抛物线y=ax2﹣![]() x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C(0,﹣2),已知B点坐标为(4,0).
x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C(0,﹣2),已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)若点M是线段BC下方的抛物线上一点,记点M到线段BC的距离为d,当d取最大值时,求出此时M点的坐标;
(3)若点P是抛物线上一点,点E是直线y=﹣x上的动点,是否存在点P、E,使以点A,点B,点P,点E为顶点的四边形是平行四边形?若存在,请直接写出点E坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2﹣
x2﹣![]() x-2;(2)M(2,-3);(3)存在;点E坐标为(
x-2;(2)M(2,-3);(3)存在;点E坐标为(![]() ,
,![]() )、(
)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)根据点B、C的坐标利用待定系数法即可求出抛物线的解析式;
(2)作MN∥y轴交BC于点N,可知![]() 的面积=
的面积=![]() =2MN=
=2MN=![]() ,
,
故当MN最大时,![]() 的面积也最大,此时M到线段BC的距离d也最大,据此可解;
的面积也最大,此时M到线段BC的距离d也最大,据此可解;
(3)假设存在,设点E的坐标为(n,-n).以点A,点B,点P,点E为顶点的平行四边形分两种情况:①以AB为边,根据A、B、E点的坐标表示出P点的坐标,将其代入抛物线线解析式中即可求出n值,从而得出点E的坐标;②以AB为对角线,根据A、B、E点的坐标表示出P点的坐标,将其代入抛物线线解析式中即可求出n值,从而得出点E的坐标.综上即可得出结论.
(1)解:由题意得c=-2,0=a×42-![]() ×4-2,
×4-2,
解得a=![]() ,
,
∴抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x-2.
x-2.
(2)解:作MN∥y轴交BC于点N,
∵![]() 的面积=
的面积=![]() =2MN=
=2MN=![]() ,
,
∴当MN最大时,![]() 的面积也最大,此时M到线段BC的距离d也最大,
的面积也最大,此时M到线段BC的距离d也最大,
设直线BC的解析式为y=kx+b,
∴![]() ,
,
解得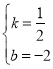 ,
,
∴y=![]() x-2,
x-2,
∴MN=![]() x-2-(
x-2-(![]() x2-
x2-![]() x-2)=-
x-2)=-![]() x2+2x=-
x2+2x=-![]() (x-2)2+2,
(x-2)2+2,
∴当x=2时,MN有最大值2,
∴M(2,-3).
∴当d取最大值时, M点的坐标是(2,-3);
(3)解:存在,理由如下:
设点 E 的坐标为 (n,n), 以点A,点B,点P,点E为顶点的平行四边形分两种情况,如图,
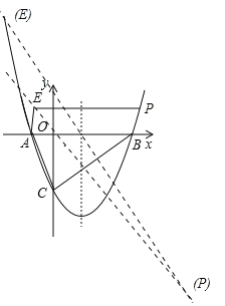
①以线段AB为边,点E在点P的左边时,
∵A(1,0),B(4,0),E(n,n),
∴P(5+n,n),
∵点P(5+n,n)在抛物线y=![]() x2-
x2-![]() x-2上,
x-2上,
∴n=![]() (5+n)2
(5+n)2![]() (5+n)2,
(5+n)2,
解得:n1=![]() , n2=
, n2=![]() ,
,
此时点E的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
以线段AB为边,点E在点P的右边时,
∵A(1,0),B(4,0),E(n,n),
∴P(n5,n),
∵点P(n5,n)在抛物线y=![]() x2
x2![]() x2上,
x2上,
∴n=![]() (n5)2
(n5)2![]() (n5)2,
(n5)2,
即n211n+36=0,
此时△=(11)24×36=23<0,
∴方程无解;
②以线段AB为对角线时,
∵A(1,0),B(4,0),E(n,n),
∴P(3n,n),
∵点P(3n,n)在抛物线y=![]() x2
x2![]() x2上,
x2上,
∴n=![]() (3n)2
(3n)2![]() (3n)2,
(3n)2,
解得:n3=![]() ,n4=
,n4=![]() ,
,
此时点E的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
综上可知:存在点P、E, 使以A、B、P、E为顶点的四边形是平行四边形, 点E坐标为(![]() ,
,![]() )、(
)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).