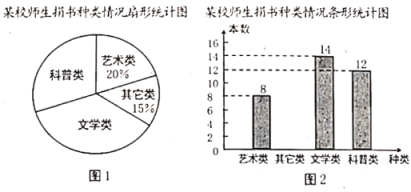
题目内容
【题目】已知:二次函数y=ax2+bx+![]() (a>0,b<0)的图象与x轴只有一个公共点A.
(a>0,b<0)的图象与x轴只有一个公共点A.
(1)当a=![]() 时,求点A的坐标;
时,求点A的坐标;
(2)求A点的坐标(只含b的代数式来表示);
(3)过点A的直线y=x+k与二次函数的图象相交于另一点B,当b≥﹣1时,求点B的横坐标m的取值范围.
【答案】(1)A(1,0);(2)(﹣![]() ,0);(3)m≥3.
,0);(3)m≥3.
【解析】
(1)由二次函数y=ax2+bx+![]() (a>0,b<0)的图象与x轴只有一个公共点A,推出△=b2-4a×
(a>0,b<0)的图象与x轴只有一个公共点A,推出△=b2-4a×![]() =b2-2a=0,再根据a=
=b2-2a=0,再根据a=![]() ,代入求出b即可;
,代入求出b即可;
(2)令y=0,求出x的值即可得出A点坐标;
(3)构建方程组求出点B的横坐标,利用二次函数的性质即可解决问题;
解:(1)∵二次函数y=ax2+bx+![]() (a>0,b<0)的图象与x轴只有一个公共点,
(a>0,b<0)的图象与x轴只有一个公共点,
∴b2﹣4a×![]() =0,
=0,
即:b2=2a,
当a=![]() 时,b2=1,
时,b2=1,
又∵b<0,
∴b=﹣1,
∴二次函数的关系式为:y=![]() x2﹣x+
x2﹣x+![]() ,
,
当y=0时,![]() x2﹣x+
x2﹣x+![]() =0,解得:x1=x2=1,
=0,解得:x1=x2=1,
∴点A(1,0),
(2)∵b2=2a,(a>0,b<0),
∴b=﹣![]()
当y=0时,ax2+bx+![]() =0,
=0,
∴x=![]() =
=![]() =﹣
=﹣![]() ,
,
∴点A的坐标为(﹣![]() ,0);
,0);
(3)将点A的坐标代入y=x+k得,k=![]() :
:
由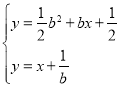 ,解得:x1=﹣
,解得:x1=﹣![]() ,x2=
,x2=![]() ,
,
∵点A的坐标为(﹣![]() ,0);
,0);
∴点B的横坐标m=![]() ,
,
∴m=![]() =2(
=2(![]() )=2(
)=2(![]() )2﹣
)2﹣![]() ,
,
∵2>0,
∴当b<![]() 时,m随
时,m随![]() 的增大而减小,
的增大而减小,
∵﹣1≤b<0,
∴![]() ≤﹣1,
≤﹣1,
∴m≥2×(﹣1﹣![]() )2﹣
)2﹣![]() =3,
=3,
即m≥3.

 ABC考王全优卷系列答案
ABC考王全优卷系列答案【题目】超越公司将某品牌农副产品运往新时代市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从超越公司出发,能否在上午10:00之前到达新时代市场?请说明理由.