题目内容
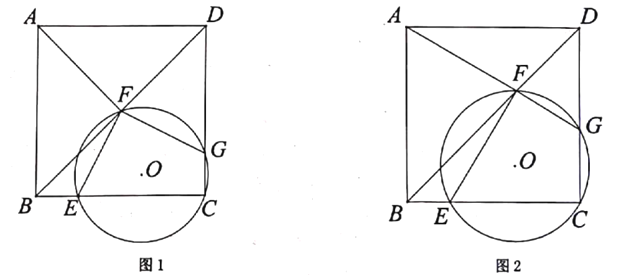
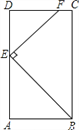
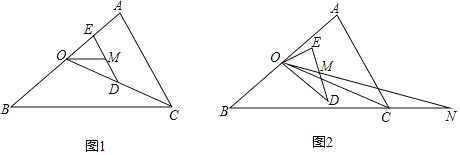
【题目】如图,OC是△ABC中AB边的中线,∠ABC=36°,点D为OC上一点,如果OD=kOC,过D作DE∥CA交于BA点E,点M是DE的中点,将△ODE绕点O顺时针旋转α度(其中0°<α<180°)后,射线OM交直线BC于点N.
(1)如果△ABC的面积为26,求△ODE的面积(用k的代数式表示);
(2)当N和B不重合时,请探究∠ONB的度数y与旋转角α的度数之间的函数关系式;
(3)写出当△ONB为等腰三角形时,旋转角α的度数.
【答案】(1)S△ODE=13k2;(2)y=α(0<α<144°);y=180°﹣α(144°<α<180°);(3)α=162°.
【解析】
(1)通过证明△ODE∽△OCA,可得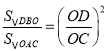 ,即可求解;
,即可求解;
(2)通过证明△OEM∽△BAC,可得∠EOM=∠ABC=36°,分两种情况讨论可求解;
(3)分四种情况讨论,由等腰三角形的性质可求解.
(1)∵OC是△ABC中AB边的中线,△ABC的面积为26,
∴S△OAC=13,
∵DE∥AC,
∴△ODE∽△OCA,∠OEM=∠OAC,
∴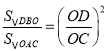 ,且OD=kOC,
,且OD=kOC,
∴S△ODE=13k2,
(2)∵△ODE∽△OCA,
∴![]() ,
,
∵OC是△ABC中AB边的中线,点M是DE的中点,
∴AB=2AO,EM=![]() DE,
DE,
∴![]() =
=![]() =
=![]() ,且∠OEM=∠OAC,
,且∠OEM=∠OAC,
∴△OEM∽△BAC,
∴∠EOM=∠ABC=36°,
如图2,当0<α<144°时,
∵∠AON=∠B+∠ONB,
∴∠AOE+∠EOM=∠B+∠ONB
∴y=α
如图3,当144°<α<180°时,
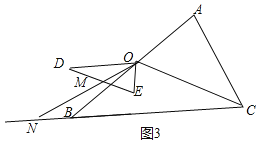
∵∠BON=∠EOM﹣∠BOE=36°﹣(180°﹣α)
∴∠NOB=α﹣144°,
∵∠BNO=∠ABC﹣∠NOB=36°﹣(α﹣144°)=180°﹣α;
(3)当0<α<144°时,若OB=ON,则∠ABC=∠BNO=36°=α,
若OB=BN,则∠ONB=![]() =72°=α,
=72°=α,
若ON=BN,则∠ABC=∠BON=36°,
∴∠ONB=180°﹣2×36°=108°=α,
当144°<α<180°时,
若OB=BN,则∠N=∠NOB=18°=180°﹣α,
∴α=162°.

 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案