题目内容
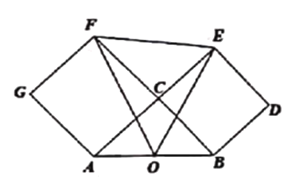
【题目】我们知道，勾股定理反映了直角三角形三条边的关系: a2+b2=c2， 而a2， b2， c2又可以看成是以a，b， c为边长的正方形的面积.如图，在Rt△ABC中，∠ACB=90°，BC=a， AC=b，O为AB的中点.分别以AC，BC 为边向△ABC外作正方形ACFG，BCED，连结OF， EF， OE，则△OEF的面积为( )
A.
B.
C.
D.
【答案】D
【解析】
作ON⊥AC于N，OM⊥BC于M，连接OC，首先证明OM、ON分别为AC、BC的中位线，得到
，
，然后分别表示出
，
和
，求和整理即可得到结果.
解：作ON⊥AC于N，OM⊥BC于M，连接OC，
∵AC⊥BC，
∴ON∥BC，OM∥AC，
∵O为AB中点，
∴OM、ON分别为AC、BC的中位线，
∴
，
，
∴
，
，
，
∴
，
故选：D.
练习册系列答案
浙江之星学业水平测试系列答案
高效智能课时作业系列答案
相关题目
