题目内容
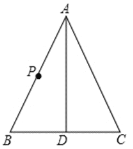
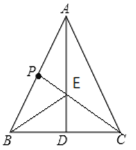
【题目】如图,在△ABC中,AB=AC, AD是△ABC 底边BC上的中线,P为AB上一点.
(1)在AD上找一点E,使得PE+EB的值最小;
(2)若P为AB的中点,当∠BPE= °时,△ABC是等边三角形.(直接写出结果)
【答案】(1)见解析;(2)90°
【解析】
(1)根据等腰三角形三线合一的性质可知AD垂直平分BC,再根据两点间距离最短的性质,连接CP交AD于点E,并连接BE,即可得到本题答案.
(2)因为P为AB的中点,要使△ABC是等边三角形,则需BC=AB,根据等腰三角形三线合一的性质,所以CP⊥AB,即∠BPE=90°.
(1)如图,点E为所求.理由如下:
连接CP交AD于点E,并连接BE
∵AB=AC, AD是△ABC 底边BC上的中线
∴AD⊥BC,且BD=CD
∴BE=CE
∵两点间线段最短
∴PE+EB=PC
∴下图中E点即为所求.
(2)90°.理由如下:
∵△ABC是等边三角形
∴BC=AB
∵P为AB的中点
∴BP=AP
∴CP⊥AB
∴∠BPE=90°.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目