题目内容
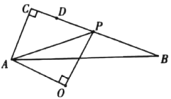
【题目】如图，在平行四边形ABCD中，连接BD，且BD＝CD，过点A作AM⊥BD于点M，过点D作DN⊥AB于点N，且DN＝
，在DB的延长线上取一点P，满足∠ABD＝∠MAP＋∠PAB，则AP＝_____.
【答案】6
【解析】根据BD=CD，AB=CD，可得BD=BA，再根据AM⊥BD，DN⊥AB，即可得到DN=AM=3
，依据∠ABD=∠MAP+∠PAB，∠ABD=∠P+∠BAP，即可得到△APM是等腰直角三角形，进而得到AP=AM=6．
∵BD=CD，AB=CD，
∴BD=BA，
又∵AM⊥BD，DN⊥AB，
∴DN=AM=3，
又∵∠ABD=∠MAP+∠PAB，∠ABD=∠P+∠BAP，
∴∠P=∠PAM，
∴△APM是等腰直角三角形，
∴AP=AM=6，
故答案为：6．
练习册系列答案
相关题目
