题目内容
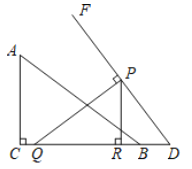
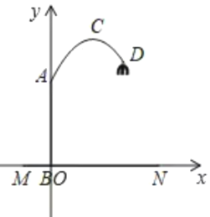
【题目】如图，一款落地灯的灯柱
垂直于水平地面
，高度为1.6米，支架部分的形状为开口向下的抛物线，其顶点
距灯柱的水平距离为0.8米，距地面的高度为2.4米，灯罩
距灯柱的水平距离为1.4米，则灯罩顶端D距地面的高度为______米．
【答案】1.95
【解析】
以点B为原点建立直角坐标系，则点C为抛物线的顶点，即可设顶点式y＝a（x0.8）2＋2.4，点A的坐标为（0，1.6），代入可得a的值，从而求得抛物线的解析式，将点D的横坐标代入，即可求点D的纵坐标就是点D距地面的高度．
解：如图，以点B为原点，建立直角坐标系．
由题意，点A（0，1.6），点C（0.8，2.4），则设顶点式为y＝a（x0.8）2＋2.4，
将点A代入得，1.6＝a（00.8）2＋2.4，解得a＝1.25，
∴该抛物线的函数关系为y＝1.25（x0.8）2＋2.4，
∵点D的横坐标为1.4，
∴代入得，y＝1.25×（1.40.8）2＋2.4＝1.95，
故灯罩顶端D距地面的高度为1.95米，
故答案为：1.95．
练习册系列答案
相关题目
