题目内容
16.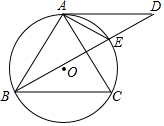 如图,⊙O为ABC的外接圆,AD为⊙O的切线,AD∥BC,BD交⊙O于E,且点E是$\widehat{AC}$的中点,连接AE.
如图,⊙O为ABC的外接圆,AD为⊙O的切线,AD∥BC,BD交⊙O于E,且点E是$\widehat{AC}$的中点,连接AE.(1)求证:AE平分∠DAC;
(2)若AD=40,BC=48,求⊙O的半径长及AE的长.
分析 (1)想办法证明∠DAE=∠ABD,∠CAE=∠ABD即可.
(2)如图,连接OA、OE,延长AO交BC于M.首先利用勾股定理求出AM,设半径为r,在Rt△COM中,利用勾股定理列出方程求出r,在Rt△AON中求出ON,在Rt△ANE中,即可求出AE.
解答 解:(1)∵点E是$\widehat{AC}$的中点,
∴∠ABE=∠CBE,
∵AD为⊙O的切线,
∴∠ABE=∠DAE,
∵∠EAC=∠CBE,
∴∠DAE=∠CAE,
∴AE平分∠DAC;
(2)如图,连接OA、OE,延长AO交BC于M.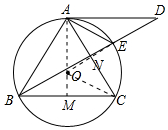
∵AD是切线,
∴OA⊥AD,
∵AD∥BC,
∴AM⊥BC,∵AB=AC,
∴BM=CM=24,∵AB=40,
∴AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=$\sqrt{4{0}^{2}-2{4}^{2}}$=32,设半径为r,
在Rt△COM中,∵OC2=OM2+CM2,
∴x2=(32-x)2+242,
∴x=25,
∴OA=25,
∵$\widehat{AE}$=$\widehat{EC}$,
∴EO⊥AC,
在Rt△AON中,∵OA=25,AN=20,
∴ON=$\sqrt{O{A}^{2}-A{N}^{2}}$=15,EN=OE-ON=10,
在Rt△ANE中,
AE=$\sqrt{A{N}^{2}+N{E}^{2}}$=$\sqrt{2{0}^{2}+1{0}^{2}}$=10$\sqrt{5}$.
点评 本题考查切线的性质、圆周角定理、勾股定理等知识,解题的关键是灵活运用所学知识,学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
6.下列各式变形正确的是( )
| A. | $\frac{x}{y}$=$\frac{{x}^{2}}{xy}$ | B. | $\frac{b}{a}$=($\frac{b}{a}$)2 | C. | $\frac{x}{y}$=$\frac{xy}{{y}^{2}}$ | D. | a3•a-2=a-6 |
7.若|a-$\frac{1}{2}$|+(2b+1)2=0,则a2+b2的值为( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 1 |
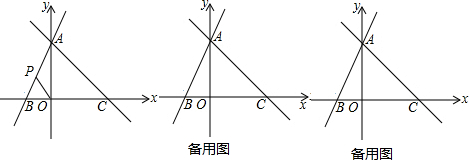
 如图,在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+12与两坐标轴分别交于A,B两点,OM⊥AB,垂足为点M.
如图,在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+12与两坐标轴分别交于A,B两点,OM⊥AB,垂足为点M.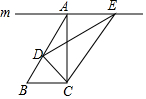 如图,在△ABC中,∠ACB=90°,过点A做直线m∥BC,过AB的中点D作DE⊥CD,DE交直线m于点E,连接CE,已知BC=5,AC=12,则AE的长为11.9.
如图,在△ABC中,∠ACB=90°,过点A做直线m∥BC,过AB的中点D作DE⊥CD,DE交直线m于点E,连接CE,已知BC=5,AC=12,则AE的长为11.9.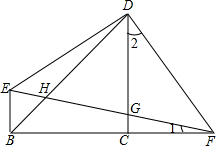 如图,等腰Rt△BCD中,∠BCD=90°,BC=CD,EB⊥BC,Rt△EDF中,∠EDF=90°,B、C、F在一条直线上,
如图,等腰Rt△BCD中,∠BCD=90°,BC=CD,EB⊥BC,Rt△EDF中,∠EDF=90°,B、C、F在一条直线上,