题目内容
7．若|a-$\frac{1}{2}$|+（2b+1）2=0，则a2+b2的值为（ ）| A． | 0 | B． | $\frac{1}{2}$ | C． | $\frac{1}{4}$ | D． | 1 |
分析 根据非负数的性质列式求出a、b的值，然后代入代数式进行计算即可得解．
解答 解：由题意得，a-$\frac{1}{2}$=0，2b+1=0，
解得a=$\frac{1}{2}$，b=-$\frac{1}{2}$，
所以，a2+b2=（$\frac{1}{2}$）2+（-$\frac{1}{2}$）2=$\frac{1}{4}$+$\frac{1}{4}$=$\frac{1}{2}$．
故选B．
点评 本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
练习册系列答案
浙江之星学业水平测试系列答案
高效智能课时作业系列答案
相关题目
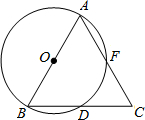如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连结AC交⊙O于点F．
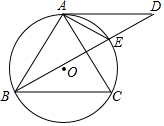如图，⊙O为ABC的外接圆，AD为⊙O的切线，AD∥BC，BD交⊙O于E，且点E是$\widehat{AC}$的中点，连接AE．