题目内容
8.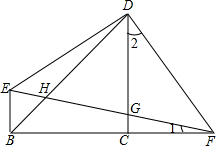 如图,等腰Rt△BCD中,∠BCD=90°,BC=CD,EB⊥BC,Rt△EDF中,∠EDF=90°,B、C、F在一条直线上,
如图,等腰Rt△BCD中,∠BCD=90°,BC=CD,EB⊥BC,Rt△EDF中,∠EDF=90°,B、C、F在一条直线上,(1)若ED=4,求S△EDF.
(2)若∠2=2∠1,求证:HF=HE+HD.
分析 (1)在正方形ABCD中,由FD与DE垂直,利用等式的性质得到一对角相等,再由一对直角相等,且AD=DC,利用AAS得到三角形DAE与三角形DCF全等,利用全等三角形对应边相等得到AE=CF,进而求得结论;
(2)在HF上取一点P,使FP=EH,连接DP,利用SAS得到三角形DEH与三角形DFP全等,利用全等三角形对应边相等,对应角相等得到DH=DP,∠EDH=∠FDP,进而确定出三角形DHP为等边三角形,利用等边三角形的性质即可得证.
解答 (1)解:过D作DA⊥BE交BE的延长线于A,
则四边形ABCD是正方形,
∴∠ADE=90°-∠EDC=∠CDF,
∴∠EDF=∠ADC=90°,
在△DAE和△DCF中,
$\left\{\begin{array}{l}{∠ADE=∠CDF}\\{∠A=∠DCF}\\{AD=CD}\end{array}\right.$,
∴Rt△DAE≌Rt△DCF(AAS),
∴AE=CF,DE=DF,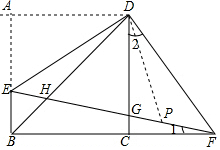
∴S△EDF=$\frac{1}{2}$DE•DF=$\frac{1}{2}×$4×4=8;
(2)证明:在HF上取一点P,使FP=EH,连接DP,
由(1)Rt△DAE≌Rt△DCF得△EDF是等腰直角三角形,
∴DE=DF,∠DEF=∠DFE=45°,
∴△DEH≌△DFP(SAS),
∴DH=DP,∠EDH=∠FDP,
在△DHE和△FHB中,
∵∠DEF=∠HBF=45°,∠EHD=∠BHF(对顶角),
∴∠EDH=∠1=$\frac{1}{2}$∠ADE=$\frac{1}{2}$(45°-∠EDH),
∴∠EDH=15°,∠FDP=15°,
∴∠HDP=90°-15°-15°=60°,
∴△DHP是等边三角形,
∴HD=HP,HF=HE+HD.
点评 此题考查了正方形的性质,全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

| A. | $\frac{1}{18}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
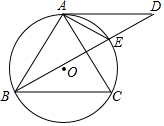 如图,⊙O为ABC的外接圆,AD为⊙O的切线,AD∥BC,BD交⊙O于E,且点E是$\widehat{AC}$的中点,连接AE.
如图,⊙O为ABC的外接圆,AD为⊙O的切线,AD∥BC,BD交⊙O于E,且点E是$\widehat{AC}$的中点,连接AE.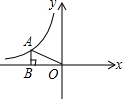 如图,点A为反比例函数 y=$\frac{k}{x}$(k≠0)图象上一点,过A作AB⊥x轴于点B,连接OA,若△ABO的面积为2,则k=-4.
如图,点A为反比例函数 y=$\frac{k}{x}$(k≠0)图象上一点,过A作AB⊥x轴于点B,连接OA,若△ABO的面积为2,则k=-4.