题目内容
【题目】如图,AD是△ABC的中线,tanB=![]() ,cosC=
,cosC=![]() ,AC=
,AC=![]()
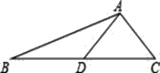
(1)求BC的长;
(2)作出△ABC的外接圆(尺规作图,保留痕迹,不写作法),并求外接圆半径.
【答案】(1)5;(2)AO=![]() .
.
【解析】
(1)过点A作AE⊥BC于点E,根据三角函数的定义和特殊角的三角函数即可得出.
(2)作AB、AC的垂直平分线,交点O即为圆心,以0A为半径作圆,即可得出△ABC的外接圆,根据sin∠ABC=sin∠AOK即可求解.
解:(1)如图过点A作AE⊥BC于点E,

∵cosC=![]() ,
,
∴∠C=45°,
在Rt△ACE中,CE=ACcosC=1,
∴AE=CE=1,
在Rt△ABE中,tanB=![]() ,即
,即![]() ,
,
∴BE=4AE=4,
∴BC=BE+CE=5.
(2)如图,⊙O就是所求作的△ABC的外接圆.

∵∠AOC=2∠ABC,∠AOK=∠COK,∴∠ABC=∠AOK,
∵sin∠AOK=sin∠ABC=![]()
由(1)可知AB=![]()
∴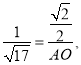
∴AO=![]() .
.

练习册系列答案
相关题目
【题目】共享单车逐渐成为市民喜爱的“绿色出行” 方式之一,今年国庆假期某一天,济川中学初三数学社团的同学们随机调查了一个社区,将这天部分出行市民使用共享单车的数据整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1) 这天部分出行市民使用共享单车次数的中位数是__________,众数是__________
(2) 这天部分出行市民平均每人使用共享单车多少次?
(3) 若该社区这天有1500人出行,请你估计这天使用共享单车次数在3次以上(含3 次)的市民有多少人?