题目内容
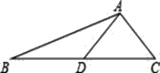
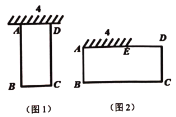
【题目】如图，校园空地上有一面墙，长度为4米，为了创建“美丽校园”，学校决定借用这面墙和20米的围栏围成一个矩形花园
，设
长为
米，矩形花园的面积为
平方米.
（1）如图1，若所围成的矩形花园边的长不得超出这面墙，求关于的函数关系式，并写出自变量的取值范围；
（2）在（1）的条件下，当为何值时，矩形花园的面积最大，最大值是多少？
（3）如图2，若围成的矩形花园的边的长可超出这面墙，求围成的矩形的最大面积.
【答案】（1）
（
）.（2）当
为4时，矩形花园ABCD的面积最大，最大值为32.（3）36.
【解析】
根据矩形的面积公式计算即可．
先求出符合题意的二次函数解析式，并化成顶点式，利用自变量的取值范围和二次函数的性质解决问题即可．
构建二次函数，利用二次函数的最值解决问题即可．
解：由题得：
，
，
则
．
x的取值范围为
．
，
又 ，
当时，s随着x的增大而增大．当
时，s的值最大，且最大
．
答：当AD为4时，矩形花园ABCD的面积最大，最大值为32．由题得：，
，
，
则
当
时，s的值最大，且最大
．
答：矩形花园ABCD的面积最大时，面积为36．
练习册系列答案
相关题目
