��Ŀ����
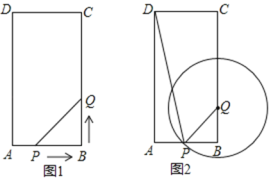
����Ŀ����֪������y1��x2��2x+c�IJ���ͼ����ͼ1��ʾ��
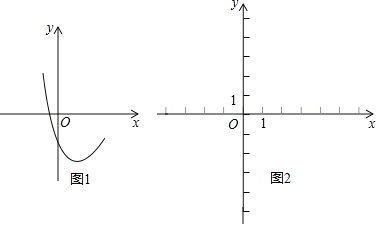
��1��ȷ��c��ȡֵ��Χ��
��2���������߾����㣨0����1������ȷ��������y1��x2��2x+c�Ľ���ʽ��
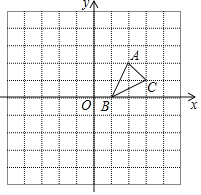
��3��������������y2��![]() ��ͼ����2�����������ϵ㣨1��a��������ͼ2��ʾֱ������ϵ�У������÷�������������2���������ߵ�ͼ������ͼ��д����y1��y2ʱ����Ӧ�Ա���x��ȡֵ��Χ��
��ͼ����2�����������ϵ㣨1��a��������ͼ2��ʾֱ������ϵ�У������÷�������������2���������ߵ�ͼ������ͼ��д����y1��y2ʱ����Ӧ�Ա���x��ȡֵ��Χ��
���𰸡���1��c��0����2��y1��x2��2x��1����3��ͼ�����������x����1��0��x��1��x��2ʱ��y1��y2����
��������
��1������ͼ1�������ߵ�ͼ���֪��c��0����������x��Ӧ�����������㣬��ˡ���0���ɴ˿����c��ȡֵ��Χ��
��2�����㣨0����1������������������м��ɵó������Ľ���ʽ��
��3������ͼ����һ���ѵ㣬��ͼ�㼴Ϊ��ͼ������Ӧ����ʽ���ɷ�����Ľ⣬�۲�ͼ��y1��y2�����㣨1����2���⣬���������������Ϊ����1��2���ͣ�2����1������x����1��y��2��x��2��y����1�ֱ����y1��x2��2x��1��y2��![]() ��֪������1��2���ͣ�2����1����y1��y2���������㣮����ͼ���֪����x����1��0��x��1��x��2ʱ��y1��y2��
��֪������1��2���ͣ�2����1����y1��y2���������㣮����ͼ���֪����x����1��0��x��1��x��2ʱ��y1��y2��
�⣺��1������ͼ���֪c��0��
��������y1��x2��2x+c��x������������
����һԪ���η���x2��2x+c��0���������ȵ�ʵ������
���ԡ�������2��2��4c��4��4c��0����c��0
����c��0��
��2����Ϊ�����߾����㣨0����1��
��x��0��y1����1����y1��x2��2x+c
��c����1
�����������ߵĽ���ʽΪy1��x2��2x��1
��3����Ϊ����������y2��![]() ��ͼ��������y1��x2��2x��1�ϵĵ㣨1��a��
��ͼ��������y1��x2��2x��1�ϵĵ㣨1��a��
��x��1��y1��a����y1��x2��2x��1����a����2
��x��1��a����2����y2��![]() ����k����2
����k����2
����y2��![]() ��
��
����y2��![]() ��ͼ����ͼ��ʾ��
��ͼ����ͼ��ʾ��
�۲�ͼ��y1��y2�����㣨1����2���⣬���������������Ϊ����1��2���ͣ�2����1��
��x����1��y2��2��x��2��y2����1��
�ֱ����y1��x2��2x��1��y��![]() ��֪������1��2���ͣ�2����1����y1��y2����������
��֪������1��2���ͣ�2����1����y1��y2����������
����ͼ���֪����x����1��0��x��1��x��2ʱ��y1��y2��


 A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�