题目内容
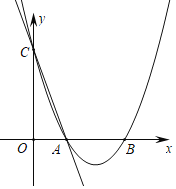
【题目】已知m,n是方程x2-6x+5=0的两个实数根,且m<n,抛物线
y=-x2+bx+c的图象经过点A(m,0)、B(0,n).
(1)求这个抛物线的解析式;
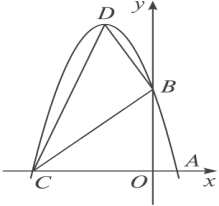
(2)设(1)中抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;
(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
【答案】(1)、y=-x2-4x+5;(2)、15;(3)、(-![]() ,0)或(-
,0)或(-![]() ,0).
,0).
【解析】
试题分析:(1)、首先求出方程的解得出点A和点B的坐标,然后利用待定系数法求出函数解析式;(2)、根据二次函数的解析式得出点C的坐标和顶点坐标,过D作x轴的垂线交x轴于M,从而求出△DMC、梯形MDBO和△BOC的面积,然后得出面积;(3)、设P点的坐标为(a,0),得出直线BC的方程,则PH与直线BC的交点坐标为(a,a+5),PH与抛物线的交点坐标为H(a,-a2-4a+5),然后根据EH=![]() EP和EH=
EP和EH=![]() EP两种情况分别求出点P的坐标.
EP两种情况分别求出点P的坐标.
试题解析:(1)、解方程x2-6x+5=0,得x1=5,x2=1.由m<n,m=1,n=5,
所以点A、B的坐标分别为A(1,0),B(0,5).将A(1,0),B(0,5)的坐标分别代入y=-x2+bx+c,
得![]() 解这个方程组得
解这个方程组得![]()
所以,抛物线的解析式为y=-x2-4x+5.
(2)、由y=-x2-4x+5,令y=0,得-x2-4x+5=0,解这个方程得x1=-5,x2=1,
所以C点的坐标为(-5,0).由顶点坐标公式计算得点D(-2,9).
过D作x轴的垂线交x轴于M.则S△DMC=![]() ×9×(5-2)=
×9×(5-2)=![]() ,
,
S梯形MDBO=![]() ×2×(9+5)=14,S△BOC=
×2×(9+5)=14,S△BOC=![]() ×5×5=
×5×5=![]() ,
,
所以,S△BCD=S梯形MDBO+S△DMC-S△BOC=14+![]() -
-![]() =15.
=15.
(3)、设P点的坐标为(a,0),
因为线段BC过B、C两点,所以BC所在的直线方程为y=x+5.
那么,PH与直线BC的交点坐标为E(a,a+5),
PH与抛物线y=-x2-4x+5的交点坐标为H(a,-a2-4a+5).
由题意,得①EH=![]() EP,即(-a2-4a+5)-(a+5)=
EP,即(-a2-4a+5)-(a+5)=![]() (a+5).
(a+5).
解这个方程,得a=-![]() 或a=-5(舍去).
或a=-5(舍去).
②EH=![]() EP,即(-a2-4a+5)-(a+5)=
EP,即(-a2-4a+5)-(a+5)=![]() (a+5),
(a+5),
解这个方程,得a=-![]() 或a=-5(舍去),
或a=-5(舍去),
∴P点的坐标为(-![]() ,0)或(-
,0)或(-![]() ,0).
,0).

 春雨教育同步作文系列答案
春雨教育同步作文系列答案