题目内容
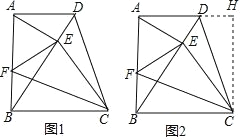
【题目】已知:如图,四边形 ABCD 中,AD∥BC,∠ABC=90°,AB=BC,AE⊥BD,EF⊥CE
(1)试证明△AEF∽△BEC;
(2)如图,过 C 点作 CH⊥AD 于 H,试探究线段 DH 与 BF 的数量关系,并说明理由;
(3)若 AD=1,CD=5,试求出 BE 的值?
【答案】(1)证明见解析;(2)DH=BF,理由见解析;(3)BE=![]() .
.
【解析】
(1)想办法证明∠AEF=∠BEC,∠FAE=∠EBC即可解决问题;
(2)结论:DH=BF.利用比例的性质首先证明AD=AF,再证明四边形ABCH是正方形即可解决问题;
(3)设正方形的边长为x,在Rt△CDH中,DH=x-1,CH=x,CD=5,可得52=x2+(x-1)2,解得x=4,再通过解直角三角形求出BE的长即可.
(1)证明:∵AE⊥BD,EF⊥CE,
∴∠AEB=∠FEC=90°,
∴∠AEF=∠BEC,
∵∠ABC=90°,
∴∠ABE+∠EBC=90°,∠ABE+∠FAE=90°,
∴∠FAE=∠EBC,
∴△AEF∽△BEC;
(2)解:结论:DH=BF.
理由:∵△AEF∽△BEC,
∴![]() ,
,
∵∠ABE=∠ABD,∠AEB=∠BAD=90°,
∴△ABE∽△DBA,
∴![]() ,
,
∴![]() ,∵BC=AB,
,∵BC=AB,
∴AF=AD,
∵∠ABC=∠BAD=∠H=90°,
∴四边形ABCH是矩形,
∵AB=BC,
∴四边形ABCH是正方形,
∴AB=AH,∵AF=AD,
∴BF=DH.
(3)设正方形的边长为x,
在Rt△CDH中,DH=x-1,CH=x,CD=5,
∴52=x2+(x-1)2,
解得x=4,
∴AB=4,AD=1,
在Rt△ABD中,BD=![]() ,
,
∵![]() ADAB=
ADAB=![]() BDAE,
BDAE,
∴AE=![]() ,
,
在Rt△AEB中,BE=![]() .
.


练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目