Question

【题目】如图，港口B位于港口A的南偏东37°方向，灯塔C恰好在AB的中点处，一艘海轮位于港口A的正南方向，港口B的正西方向的D处，它沿正北方向航行5km到达E处，测得灯塔C在北偏东45°方向上，这时，E处距离港口A有多远？（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

Answer 1

【答案】解：如图作CH⊥AD于H．设CH=xkm，
在Rt△ACH中，∠A=37°，∵tan37°= ，
∴AH= = ，
在Rt△CEH中，∵∠CEH=45°，
∴CH=EH=x，
∵CH⊥AD，BD⊥AD，
∴CH∥BD，
∴ = ，
∵AC=CB，
∴AH=HD，
∴ =x+5，
∴x= ≈15，
∴AE=AH+HE= +15≈35km，
∴E处距离港口A有35km．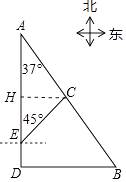

【解析】如图作CH⊥AD于H．设CH=xkm，在Rt△ACH中，可得AH= = ，在Rt△CEH中，可得CH=EH=x，由CH∥BD，推出 = ，由AC=CB，推出AH=HD，可得 =x+5，求出x即可解决问题．
【考点精析】关于本题考查的关于方向角问题，需要了解指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角才能得出正确答案．