题目内容
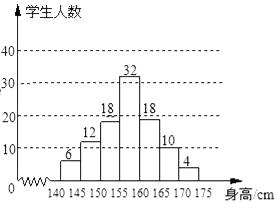
【题目】某学校为了解该校七年级学生的身高情况，抽样调查了部分同学，将所得数据处理后，制成扇形统计图和频数分布直方图（部分）如下（每组只含最低值不含最高值，身高单位：cm，测量时精确到1cm）：
（1）请根据所提供的信息计算身高在160～165cm范围内的学生人数，并补全频数分布直方图；
（2）样本的中位数在统计图的哪个范围内？
（3）如果上述样本的平均数为157cm，方差为0.8；该校八年级学生身高的平均数为159cm，方差为0.6，那么（填“七年级”或“八年级”）学生的身高比较整齐．
【答案】
（1）
解：总数为：32÷32%=100，则160﹣165的频数为：100﹣6﹣12﹣18﹣32﹣10﹣4=18或100×18%=18．
根据数据正确补全频数分布直方图，如下图：
（2）
解：第50和51个数的平均数在155～160cm的范围内，所以样本的中位数在155～160cm的范围内；
（3）八年级
【解析】（3）方差越小，数据的离散程度越小，所以八年级学生的身高比较整齐．
故答案为：八年级．
（1）根据155﹣160的频数和百分比求总数．从而求出160﹣165的频数，根据数据正确补全频数分布直方图即可；（2）根据中位数的确定方法求解；（3）利用方差的意义判断．
练习册系列答案
相关题目
【题目】某工厂计划生产A，B两种产品共10件，其生产成本和利润如下表：
A种产品 | B种产品 | |
成本（万元∕件） | 3 | 5 |
利润（万元∕件） | 1 | 2 |
（1）若工厂计划获利14万元，问A，B两种产品应分别生产多少件？
（2）若工厂投入资金不多于44万元，且获利多于14万元，问工厂有哪几种生产方案？
（3）在（2）条件下，哪种方案获利最大？并求最大利润．
