题目内容
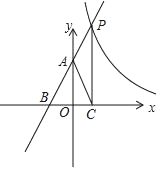
【题目】已知,如图所示直线y=kx+2(k≠0)与反比例函数y=![]() (m≠0)分别交于点P,与y轴、x轴分别交于点A和点B,且cos∠ABO=
(m≠0)分别交于点P,与y轴、x轴分别交于点A和点B,且cos∠ABO=![]() ,过P点作x轴的垂线交于点C,连接AC,
,过P点作x轴的垂线交于点C,连接AC,
(1)求一次函数的解析式.
(2)若AC是△PCB的中线,求反比例函数的关系式.
【答案】(1)y=2x+2;(2)y=![]() .
.
【解析】
(1)由cos∠ABO=![]() ,可得到tan∠ABO=2,从而可得到k=2;
,可得到tan∠ABO=2,从而可得到k=2;
(2)先求得A、B的坐标,然后依据中点坐标公式可求得点P的坐标,将点P的坐标代入反比例函数的解析式可求得m的值.
(1)∵cos∠ABO=![]() ,
,
∴tan∠ABO=2.又∵OA=2
∴OB=1.B(-1,0)代入y=kx+2得k=2
∴一次函数的解析式为y=2x+2.
(2)当x=0时,y=2,
∴A(0,2).
当y=0时,2x+2=0,解得:x=﹣1.
∴B(﹣1,0).
∵AC是△PCB的中线,
∴P(1,4).
∴m=xy=1×4=4,
∴反例函数的解析式为y=![]() .
.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目