Question

【题目】已知：如图，在半径是4的⊙O中，AB、CD是两条直径，M是OB的中点，CM的延长线交⊙O于点E，且EM＞MC，连接DE，DE=．

（1）求证：△AMC∽△EMB；

（2）求EM的长；

（3）求sin∠EOB的值．

Answer 1

【答案】（1）详见解析；（2）EM=4；（3）sin∠EOB=．

【解析】

（1）连接A、C，E、B点，那么只需要求出△AMC和△EMB相似，即可求出结论，根据圆周角定理可推出它们的对应角相等，即可得△AMC∽△EMB；
（2）根据圆周角定理，结合勾股定理，可以推出EC的长度，根据已知条件推出AM、BM的长度，然后结合（1）的结论，很容易就可求出EM的长度；
（3）过点E作EF⊥AB，垂足为点F，通过作辅助线，解直角三角形，结合已知条件和（1）（2）所求的值，可推出Rt△EOF各边的长度，根据锐角三角函数的定义，便可求得sin∠EOB的值．

（1）证明：连接AC、EB，如图1，

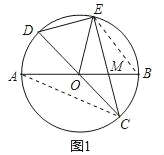
∵∠A=∠BEC，∠B=∠ACM，

∴△AMC∽△EMB；

（2）解：∵DC是⊙O的直径，

∴∠DEC=90°，

∴DE2+EC2=DC2，

∵DE=，CD=8，且EC为正数，

∴EC=7，

∵M为OB的中点，

∴BM=2，AM=6，

∵AMBM=EMCM=EM（EC﹣EM）=EM（7﹣EM）=12，且EM＞MC，

∴EM=4；

（3）解：过点E作EF⊥AB，垂足为点F，如图2，

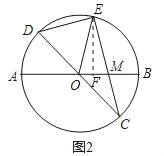
∵OE=4，EM=4，

∴OE=EM，

∴OF=FM=1，

∴EF==，

∴sin∠EOB==．