ЬтФПФкШн
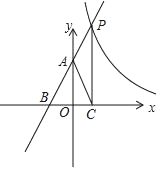
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=BCЃЌжБЯпMNОЙ§ЕуCЃЌЧвADЁЭMNгкDЃЌBEЁЭMNгкEЃЎ

ЃЈ1ЃЉЕБжБЯпMNШЦЕуCа§зЊЕНЭМЃЈ1ЃЉЕФЮЛжУЪБЃЌЯдШЛгаЃКDE=AD+BEЃЛЧыжЄУїЃЎ
ЃЈ2ЃЉЕБжБЯпMNШЦЕуCа§зЊЕНЭМЃЈ2ЃЉЕФЮЛжУЪБЃЌЧѓжЄЃКDE=AD-BEЃЛ
ЃЈ3ЃЉЕБжБЯпMNШЦЕуCа§зЊЕНЭМЃЈ3ЃЉЕФЮЛжУЪБЃЌЪдЮЪЃЈ2ЃЉжаDEЁЂADЁЂBEЕФЙиЯЕЛЙГЩСЂТ№ЃПШєГЩСЂЃЌЧыжЄУїЃЛШєВЛГЩСЂЃЌЫќУЧгжОпгадѕбљЕФЕШСПЙиЯЕЃПЧыжЄУїЃЎ
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉDE=BEЉADЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉжЄУїЁїADCЁеЁїCEBЃЌШЛКѓРћгУШЋЕШШ§НЧаЮЕФаджЪМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉжЄУїЁїADCЁеЁїCEBЃЌШЛКѓРћгУШЋЕШШ§НЧаЮЕФаджЪМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЕБжБЯпMNШЦЕуCа§зЊЕНЭМЃЈ3ЃЉЕФЮЛжУЪБЃЌШдШЛЁїADCЁеЁїCEBЃЌШЛКѓРћгУШЋЕШШ§НЧаЮЕФаджЪПЩвдЕУЕНDE=BEЉADЃЎ
ЃЈ1ЃЉЁпЁїABCжаЃЌЁЯACB=90ЁуЃЌЁрЁЯACD+ЁЯBCE=90ЁуЃЌ
гжжБЯпMNОЙ§ЕуCЃЌЧвADЁЭMNгкDЃЌBEЁЭMNгкEЃЌ
ЁрЁЯADC=ЁЯCEB=90ЁуЃЌЁрЁЯACD+ЁЯDAC=90ЁуЃЌЁрЁЯBCE=ЁЯDACЃЌ
дкЁїADCКЭЁїCEBжаЃЌ
Ёп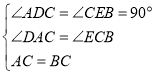 ЃЌ
ЃЌ
ЁрЁїADCЁеЁїCEBЃЈAASЃЉЃЌЁрCD=BEЃЌAD=CEЃЌЁрDE=CD+CE=AD+BEЃЛ
ЃЈ2ЃЉЁпЁїABCжаЃЌЁЯACB=90ЁуЃЌжБЯпMNОЙ§ЕуCЃЌЧвADЁЭMNгкDЃЌBEЁЭMNгкEЃЌ
ЁрЁЯADC=ЁЯCEB=90ЁуЃЌЁЯACD+ЁЯBCE=ЁЯBCE+ЁЯCBE=90ЁуЃЌ
ЁрЁЯACD=ЁЯCBEЃЎ
ЖјAC=BCЃЌЁрЁїADCЁеЁїCEBЃЌЁрCD=BEЃЌCE=ADЃЌЁрDE=CEЉCD=ADЉBEЃЛ
ЃЈ3ЃЉШчЭМ3ЃЎ
ЁпЁїABCжаЃЌЁЯACB=90ЁуЃЌжБЯпMNОЙ§ЕуCЃЌЧвADЁЭMNгкDЃЌBEЁЭMNгкEЃЌЁрЁЯADC=ЁЯCEB=90ЁуЃЌЁЯACD+ЁЯBCE=ЁЯBCE+ЁЯCBE=90ЁуЃЌЁрЁЯACD=ЁЯCBEЃЎ
ЁпAC=BCЃЌЁрЁїADCЁеЁїCEBЃЌЁрCD=BEЃЌCE=ADЃЌЁрDE=CDЉCE=BEЉADЃЛ
DEЁЂADЁЂBEжЎМфЕФЙиЯЕЮЊDE=BEЉADЃЎ