题目内容
【题目】如图1,△ABC中,AB=AC,∠BAC=90°,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上.请解答下列问题:
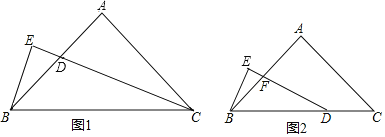
(1)图中与∠DBE相等的角有: ;
(2)直接写出BE和CD的数量关系;
(3)若△ABC的形状、大小不变,直角三角形BEC变为图2中直角三角形BED,∠E=90°,且∠EDB=![]() ∠C,DE与AB相交于点F.试探究线段BE与FD的数量关系,并证明你的结论.
∠C,DE与AB相交于点F.试探究线段BE与FD的数量关系,并证明你的结论.
【答案】(1)∠ACE和∠BCD;
(2)BE=![]() CD;
CD;
(3)BE=![]() DF,证明见解析
DF,证明见解析
【解析】
(1)根据三角形内角和定理得到∠DBE=∠ACE,根据角平分线的定义得到∠BCD=∠ACE,得到答案;
(2)延长BE交CA延长线于F,证明△CEF≌△CEB,得到FE=BE,证明△ACD≌△ABF,得到CD=BF,证明结论;
(3)过点D作DG∥CA,交BE的延长线于点G,与AE相交于H,分别证明△BGH≌△DFH、△BDE≌△GDE,根据全等三角形的性质解答即可.
解:(1)∵BE⊥CD,
∴∠E=90°,
∴∠E=∠BAC,又∠EDB=∠ADC,
∴∠DBE=∠ACE,
∵CD平分∠ACB,
∴∠BCD=∠ACE,
∴∠DBE=∠BCD,
故答案为:∠ACE和∠BCD;
(2)延长BE交CA延长线于F,
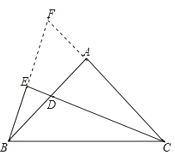
∵CD平分∠ACB,
∴∠FCE=∠BCE,
在△CEF和△CEB中,
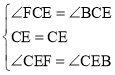 ,
,
∴△CEF≌△CEB(ASA),
∴FE=BE,
在△ACD和△ABF中,
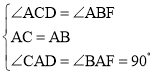 ,
,
∴△ACD≌△ABF(ASA),
∴CD=BF,
∴BE=![]() CD;
CD;
(3)BE=![]() DF
DF
证明:过点D作DG∥CA,交BE的延长线于点G,与AE相交于H,
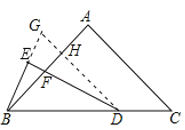
∵DG∥AC,
∴∠GDB=∠C,∠BHD=∠A=90°,
∵∠EDB=![]() ∠C,
∠C,
∴∠EDB=∠EDG=![]() ∠C,
∠C,
∵BE⊥ED,
∴∠BED=90°,
∴∠BED=∠BHD,
∵∠EFB=∠HFD,
∴∠EBF=∠HDF,
∵AB=AC,∠BAC=90°,
∴∠C=∠ABC=45°,
∵GD∥AC,
∴∠GDB=∠C=45°,
∴∠GDB=∠ABC=45°,
∴BH=DH,
在△BGH和△DFH中,
 ,
,
∴△BGH≌△DFH(ASA)
∴BG=DF,
∵在△BDE和△GDE中,
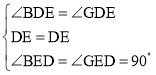 ,
,
∴△BDE≌△GDE(ASA)
∴BE=EG,
∴BE=![]() .
.