题目内容
【题目】设函数f(x)= ![]() ,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x2+y2+2x+2y在D上的最小值为 .
,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x2+y2+2x+2y在D上的最小值为 .
【答案】﹣ ![]()
【解析】解:当x>0时,f′(x)= ![]() , 则f′(1)=1,所以曲线y=f(x)及该曲线在点(1,0)处的切线为y=x﹣1,
, 则f′(1)=1,所以曲线y=f(x)及该曲线在点(1,0)处的切线为y=x﹣1,
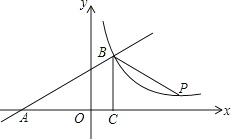
D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域如下图阴影部分.
而z=x2+y2+2x+2y=(x+1)2+(y+1)2﹣2,
表示以(﹣1,﹣1)为圆心,以(﹣1,﹣1)与阴影部分内的点为半径的平方再减2,
显然(﹣1,﹣1)到直线AC的距离最小,
由C(﹣ ![]() ,0),A(0,﹣1)得AC的方程是:2x+y+1=0,
,0),A(0,﹣1)得AC的方程是:2x+y+1=0,
此时,r=d= ![]() =
= ![]() ,r2=
,r2= ![]() ,
,
故z的最小值是 ![]() ﹣2=﹣
﹣2=﹣ ![]() ,
,
所以答案是:﹣ ![]() .
.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目