题目内容
【题目】如图，F1 ， F2分别是双曲线 
的左、右焦点，过F1的直线l与双曲线分别交于点A，B，且A（1， 
），若△ABF2为等边三角形，则△BF1F2的面积为（ ）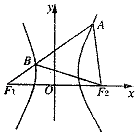 
A.1
B.
C.
D.2
【答案】C
【解析】解：根据双曲线的定义，可得|AF1|﹣|AF2|=2a， ∵△ABF2是等边三角形，即|AF2|=|AB|
∴|BF1|=2a
又∵|BF2|﹣|BF1|=2a，
∴|BF2|=|BF1|+2a=4a，
∵△BF1F2中，|BF1|=2a，|BF2|=4a，∠F1BF2=120°
∴|F1F2|2=|BF1|2+|BF2|2﹣2|BF1||BF2|cos120°
即4c2=4a2+16a2﹣2×2a×4a×（﹣ 
）=28a2 ，
解得c2=7a2 ，
∴b2=c2﹣a2=6a2 ， 所以双曲线方程为 
﹣ 
=1，
又A（1， 
），在双曲线上，所以 
=1，解得a= 
．
所以△BF1F2的面积为 
= 
= ，
故选C．
阅读快车系列答案
【题目】已知抛物线E：y2=4x的准线为l，焦点为F，O为坐标原点．
（1）求过点O，F，且与l相切的圆的方程；
（2）过F的直线交抛物线E于A，B两点，A关于x轴的对称点为A′，求证：直线A′B过定点．
【题目】某网络营销部门为了统计某市网友2016年12月12日的网购情况，从该市当天参与网购的顾客中随机抽查了男女各30人，统计其网购金额，得到如下频率分布直方图：
网购达人 | 非网购达人 | 合计 | |
男性 | 30 | ||
女性 | 12 | 30 | |
合计 | 60 |
若网购金额超过2千元的顾客称为“网购达人”，网购金额不超过2千元的顾客称为“非网购达人”．
（Ⅰ）若抽取的“网购达人”中女性占12人，请根据条件完成上面的2×2列联表，并判断是否有99%的把握认为“网购达人”与性别有关？
（Ⅱ）该营销部门为了进一步了解这60名网友的购物体验，从“非网购达人”、“网购达人”中用分层抽样的方法确定12人，若需从这12人中随机选取3人进行问卷调查．设ξ为选取的3人中“网购达人”的人数，求ξ的分布列和数学期望．
（参考公式： 
，其中n=a+b+c+d）
P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
