جâؤ؟ؤعبف
،¾جâؤ؟،؟بدصوشؤ¶ءدآأوµؤ²ؤءد£¬حê³ةسذ¹طختجâ£؛
²ؤءد£؛شعر§د°¾ّ¶شضµت±£¬خزأازرءث½â¾ّ¶شضµµؤ¼¸؛خزâزه£¬بç|5-3|±يت¾5،¢3شعتضلةد¶شس¦µؤء½µمض®¼نµؤ¾àہ룻سضبç|5+3|=|5-£¨-3£©|£¬ثùزش|5+3|±يت¾5،¢-3شعتضلةد¶شس¦µؤء½µمض®¼نµؤ¾àہë،£زٍ´ث£¬ز»°مµط£¬µمA,Bشعتضلةد·ض±ً±يت¾سذہيتa,b£¬ؤاأ´A,Bض®¼نµؤ¾àہ루ز²¾حتادك¶خABµؤ³¤¶ب£©؟ة±يت¾خھ|a-b|،£
زٍ´ثخزأا؟ةزشسأ¾ّ¶شضµµؤ¼¸؛خزâزه°´بçدآ·½·¨اَ![]() µؤ×îذ،ضµ£»
µؤ×îذ،ضµ£»
![]() ¼´تضلةدxسë1¶شس¦µؤµمض®¼نµؤ¾àہ룬
¼´تضلةدxسë1¶شس¦µؤµمض®¼نµؤ¾àہ룬![]() ¼´تضلةدxسë2¶شس¦µؤµمض®¼نµؤ¾àہ룬°رصâء½¸ِ¾àہëشعح¬ز»¸ِتضلةد±يت¾³ِہ´£¬ب»؛َ°ر¾àہëدà¼س¼´؟ةµأشت½µؤضµ.
¼´تضلةدxسë2¶شس¦µؤµمض®¼نµؤ¾àہ룬°رصâء½¸ِ¾àہëشعح¬ز»¸ِتضلةد±يت¾³ِہ´£¬ب»؛َ°ر¾àہëدà¼س¼´؟ةµأشت½µؤضµ.
ةèA،¢B،¢Pبµم¶شس¦µؤت·ض±ًتا1،¢2،¢x.
µ±1،ـx،ـ2ت±£¬¼´Pµمشعدك¶خABةد£¬´ثت±![]() £»
£»
µ±x£¾2ت±£¬¼´PµمشعBµمسز²à£¬´ثت±![]() £½ PA£«PB£½AB£«2PB£¾AB£»
£½ PA£«PB£½AB£«2PB£¾AB£»
µ±x £¼1ت±£¬¼´PµمشعAµم×َ²à£¬´ثت±![]() £½PA£«PB£½AB£«2PA£¾AB£»
£½PA£«PB£½AB£«2PA£¾AB£»
×غةد؟ةضھ£¬µ±1،ـx،ـ2ت±£¨Pµمشعدك¶خABةد£©£¬![]() ب،µأ×îذ،ضµخھ1£®
ب،µأ×îذ،ضµخھ1£®
![]()
![]()
![]()
اëؤمسأةدأوµؤث¼؟¼·½·¨½ل؛دتضلحê³ةزشدآختجâ£؛
£¨1£©آْ×م![]() µؤxµؤب،ضµ·¶خ§تا ،£
µؤxµؤب،ضµ·¶خ§تا ،£
£¨2£©اَ![]() µؤ×îذ،ضµخھ £¬×î´َضµخھ ،£
µؤ×îذ،ضµخھ £¬×î´َضµخھ ،£
±¸سأح¼£؛
![]()
![]()
،¾´ً°¸،؟£¨1£©x<-3»ٍx£¾4£»£¨2£©-3£¬3.
،¾½âخِ،؟
£¨1£©¸ù¾فجâزâ؟ة·ضبضضاé؟ِجضآغ£¬µ±x<-3ت±£¬µ±-3،ـx،ـ4ت±£¬µ±x£¾4ت±£¬·ض±ً»¯¼ٍ¾ّ¶شضµ£¬²¢شعب،ضµ·¶خ§ؤعسë7×÷±ب½د¼´؟ةµأ³ِ½ل¹û£»
£¨2£©·ضµ±x£¾-1ت±£¬µ±-1،ـx،ـ2£¬µ±x£¾2ت±بضضاé؟ِجضآغ£¬شعب،ضµ·¶خ§ؤعاَ½ل¹ûµؤ×î´َضµ؛ح×îذ،ضµ.
½â£؛£¨1£©سة![]() £¬شعتضلةد±يت¾-3؛ح4ء½µم£¬
£¬شعتضلةد±يت¾-3؛ح4ء½µم£¬
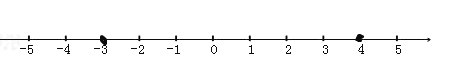
µ±x<-3ت±£¬![]() >7;
>7;
µ±-3،ـx،ـ4ت±£¬![]() .
.
µ±x£¾4ت±£¬![]() .
.
¹تµ±x<-3»ٍx£¾4ت±![]() .
.
£¨2£©![]()
µ±x£¼-1£¬![]()
µ±-1،ـx،ـ2£¬![]() £¬´ثت±µ±x=2ت±£¬ب،µأ×î´َضµ3£¬µ±x=-1ت±£¬ب،µأ×îذ،ضµ-3£»
£¬´ثت±µ±x=2ت±£¬ب،µأ×î´َضµ3£¬µ±x=-1ت±£¬ب،µأ×îذ،ضµ-3£»
µ±x£¾2ت±£¬![]() .
.
¹ت![]() µؤ×îذ،ضµخھ-3£¬×î´َضµخھ3.
µؤ×îذ،ضµخھ-3£¬×î´َضµخھ3.