题目内容
【题目】如图,在△ABC中,高AD和BE交于点H,且∠1=∠2=22.5°,下列结论:①∠1=∠3;②BD+DH=AB;③2AH=BH;④若CD=![]() ,则BH=3;⑤若DF⊥BE于点F,则AE-FH=DF;正确的有( )个.
,则BH=3;⑤若DF⊥BE于点F,则AE-FH=DF;正确的有( )个.

A. 5B. 4C. 3D. 2
【答案】C
【解析】
根据角平分线、高、等腰直角三角形的性质,全等三角形的性质和判定,矩形的判定和性质依次判断即可得出答案.
解:①∵∠1=∠2=22.5°,
又∵AD是高,
∴∠2+∠C=∠3+∠C,
∴∠2=∠3,
∴∠1=∠3,故①正确;
②∵∠1=∠2=22.5°,
∴∠ABD=∠BAD=45°,
∴AD=BD,
又∵∠2=∠3,∠ADB=∠ADC,
∴△BDH≌△ADC,
∴DH=CD,
∵∠1=∠2,BE⊥AC,
∴AB=BC,
∴BD+DH=AB,故②正确;
③无法证明;
④无法证明;
⑤作DG⊥AC于G,
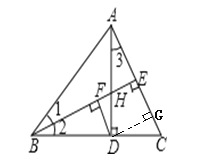
∵BE⊥AC,DF⊥BE,DG⊥AC,
∴四边形EFDG是矩形,
∴DF=EG,
∵BE⊥AC,DF⊥BE,DG⊥AC,
∴∠3+∠AHE=∠3+∠C=∠FDH+∠FHD,∠DFH=∠DGC=90°,
∵∠AHE=∠FHD,
∴∠C=∠FHD,
由②得,DH=CD,
∴△DFH≌△DGC,
∴FH=CG,
∴EC-CG=EG,即EC-FH=DF,
∵AB=BC,BE⊥AC,
∴AE=EC,
∴AE-FH=DF,故⑤正确.
故选:C.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目