题目内容
【题目】如图,AB为⊙O的直径,点C在⊙O 上,点P是直径AB上的一点,(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.
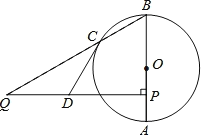
(1)点D在线段PQ上,且DQ=DC.求证:CD是⊙O的切线;
(2)若sin∠Q=![]() ,BP=6,AP=2,求QC的长.
,BP=6,AP=2,求QC的长.
【答案】(1)见解析;(2)![]()
【解析】试题分析:
(1)连接OC,由DC=DQ可得∠Q=∠DCQ,由OC=OB可得∠OCB=∠OBC,由PQ⊥AB于点P可得∠QPB=90°,从而可得∠Q+∠OBC=90°,即可得到∠DCQ+∠OCB=90°,从而可得∠OCD=90°,即可由此得到CD是⊙O的切线;
(2)由BP=6,∠QPB=90°,sin∠Q=![]() 易得BQ=10,由BP=6,AP=2易得AB=8,连接AC,易证△ABC∽△QBP,由相似三角形对应边成比例即可求得BC的长,再由BQ-BC即可求得QC的长了.
易得BQ=10,由BP=6,AP=2易得AB=8,连接AC,易证△ABC∽△QBP,由相似三角形对应边成比例即可求得BC的长,再由BQ-BC即可求得QC的长了.
试题解析:
(1)如图,连结OC.
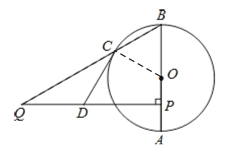
∵DQ=DC,
∴∠Q=∠QCD.
∵OC=OB,
∴∠B=∠OCB.
∵QP⊥BP,
∴∠QPB=90° ,即∠B+∠Q=90°,
∴∠QCD+∠OCB=90°,
∴∠OCD=90°,
∴CD⊥OC,即CD是⊙O的切线;
(2)如图,连结AC,
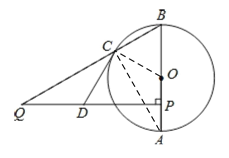
∵BP=6,AP=2,
∴AB=8,
∵在Rt△BQP中,sinQ=![]() ,
,
∴BQ=10,
连接AC,
∵AB是是⊙O的直径,
∴∠ACB=∠QPB=90°,
又∵∠B=∠B,
∴△ABC∽△QBP,
∴![]() ,即
,即![]() ,
,
∴BC=![]() ,
,
∴CQ=BQ-BC=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目